Resonance frequency measurement using a interferometric method

Team Members

• Nakarin Jayjong
• Joel Auccapuclla
• Xiaoyu Nie
• Haotian Song

Introduction

Interferometers since their invention have been a great tool for experimental physics. Applications cover a wide spectrum of fields such as astronomy, fiber optics, seismology, seismology, velocimetry to say the least. The precision of measurement of small displacements is the key factor, take LIGO as an example. Another important factor is the convenience to set up an interferometer and the low complexity in terms of equipment. This study study aims to measure the resonance frequency of a system, a transducer attached to a mirror, using a Michelson interferometer.

Theory

Our Michelson interferometer setup used a laser, a beam splitter, two mirrors, and a photometer, illustrated in Figure 3. The light propagates from the source to the beam splitter where approximately 50% of the incident light is transmitted and approximately 50% of it is reflected at a right angle. The transmitted light continues to propagate as the reference plane wave to the stationary mirror where it is fully reflected back towards the beam splitter. The reflected light propagates as the target plane wave to the mirror attached to the oscillating loudspeaker. The two waves then recombine at the beam splitter and interfere based on their relative phases based on the idea that the phase shift of the target plane wave varies with the instantaneous position of the speaker mirror combination. Consider a situation in which we setup our interferometer such that no phase shift corresponds to the equilibrium position of the speaker-mirror combination. At this position, we expect constructive interference at the photometer. Likewise, for every λ/2 change in displacement, we expect constructive interference at the photometer because the path length travelled by the target plane wave varies by some integral multiple of λ. Thus, the phase shift is an even multiple of π and the two waves remain in phase. Similarly, when the path length traveled is some odd multiple of λ/4, the phase shift is an odd multiple of π and the two waves interfere destructively.

Consider two coherent waves with the same amplitude A and same frequency $\omega$ that have paths $x_{1}$ and $x_{2}$ emitted from different sources that meet together at a point. The net wave at that point can then be given as the real part of the equation

$\psi =Ae^{i(kx_{1}-\omega t}+Ae^{i(kx_{2}-\omega t)}=Ae^{-i\omega t}e^{ik{\frac {(x_{1}+x_{2})}{2}}}[e^{ik{\frac {(x_{1}-x_{2})}{2}}}e^{-ik{\frac {(x_{1}-x_{2})}{2}}}]=2Acos[k({\frac {x_{1}-x_{2}}{2}})]e^{i[k{\frac {(x_{1}+x_{2})}{2}}-\omega t]}$

where the wave number $k=2\pi /\lambda$, $\lambda$ is the wavelength of the waves, and c is the phase velocity. The time-averaged intensity of the combined wave is then proportional to the square of the its amplitude. That is,

$I\propto cos^{2}[\pi ({\frac {p_{2}-p_{1}}{\lambda }})]=cos^{2}[2\pi ({\frac {p_{2}}{\lambda }}-\theta )]$

where $\theta$ is a constant. Now suppose the mirror that the $p_{2}$ beam is incident to oscillates harmonically back and forth with a frequency $f$ and a displacement $B$. Then, $p_{2}=p_{2}(0)+Bsin(2\pi ft)$ and the intensity of the detected light varies with time as

$I=A^{2}cos^{2}[2\pi ({\frac {Bsin(2\pi ft)}{\lambda }}-\theta ')]$

Note that the frequency of oscillations is itself a sinusoid, meaning that there will be turnaround points in the oscillations.

Experimental setup

As our main source for this experiment, we used a laser diode of wavelength 658.9 nm (as we can see in Figure 6 in the following section). Most red laser diodes are based on either GaInP or AlGaInP, this means we have two semiconductor materials. For one particular configuration, it will allow current flow and produce light amplification. The diode laser is powered by a power supply, see the left top size of Figure 3. Also, the beam coming out of the diode is divergent so an aspheric lens (C110TMD-A) is used to collimate it, while the collimation tube of laser diode is mounted on a homemade aluminum holder as shown in Figure 1.

Figure 1: Homemade laser diode.

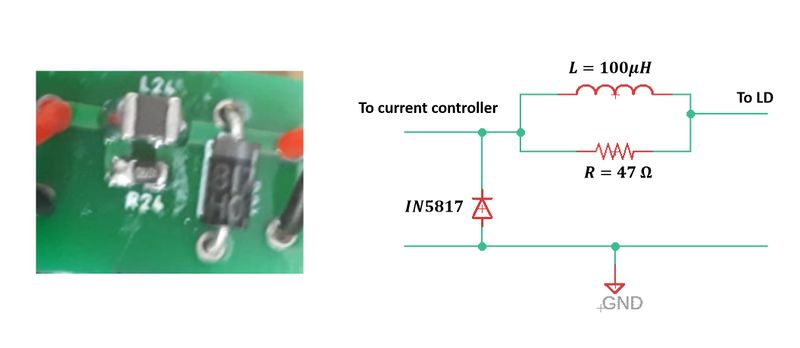
In order to prevent the reverse current through the laser diode, and protect against turn-on transients or spikes in current, we use a protection circuit that includes a resistor, an inductor, and a Schottky diode as shown in Figure 2.

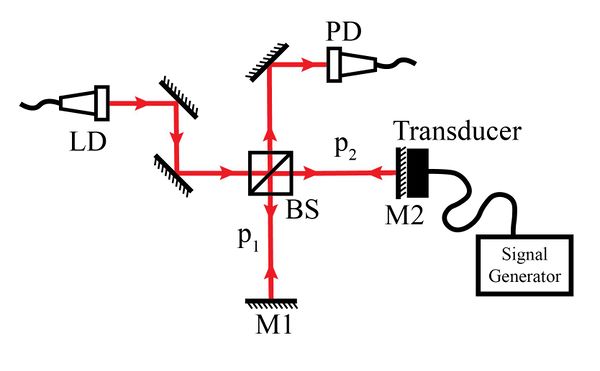
Figure 2: Protection circuit for laser diode.

Our Michelson interferometer consists of a beam splitter BS, which is used to split the laser beam into two beams, and two mirrors M1 and M2. The reflected beam goes to a fixed mirror M1 while the transmitted beam goes to the movable mirror M2. A transducer is attached, using tape, to the mirror M2. The transducer is powered by a signal generator (Aglient 33220A) that is used to vary the vibrating frequency of the mirror. A photodiode PD is used to detect the signal of interference fringes. The schematic Michelson interferometer is shown in Figure 3.

Figure 3: Schematic figure of Michelson interferometer. LD is a laser diode, BS is a beam splitter, M1 and M2 are mirrors, PD is a photodiode, and vibration transducer which is driven by a signal generator.

The experimental setup Michelson interferometer is shown in figure 4.

Figure 4: Experimental setup of Michelson interferometer.

The interference fringes of the Michelson interferometer are observed when the transducer is turned off in Figure 5.

Figure 5: Interference fringes which are observed when the transducer is turned off

Experiment Results

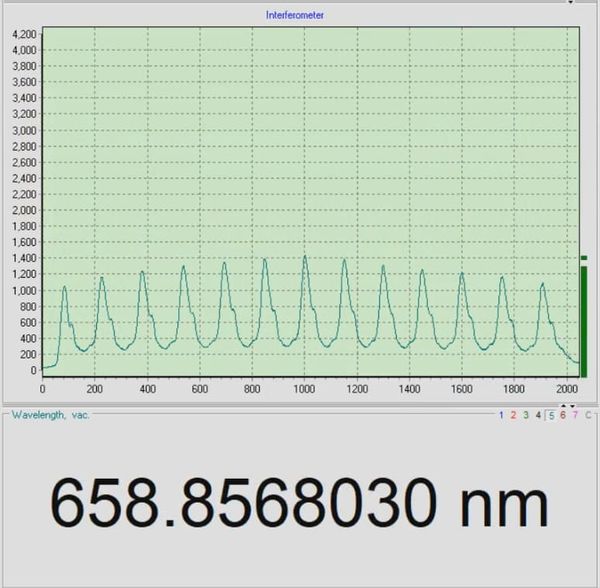
Before we started setting up our interferometer, we measured the wavelength of the laser by an Anstrom WS-7 wavemeter, the wavelength is about 658.9 nm, see Figure 6. Even more, this graph tells us that the Mitsubishi LD is in a single-mode regime, so we proceeded to build the interferometer.

Figure 6: The Wavelength measurement of the Mitsubishi Laser Diode.

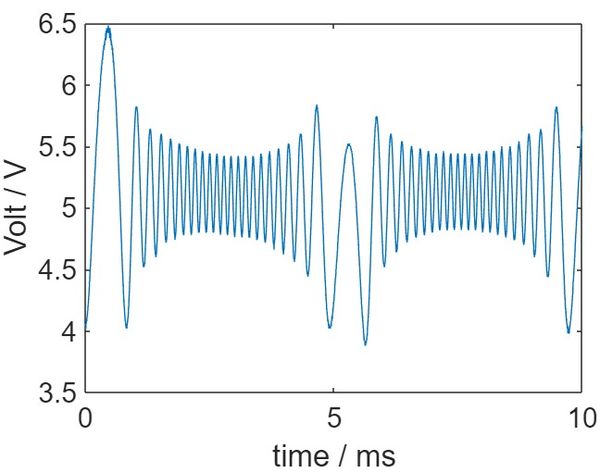
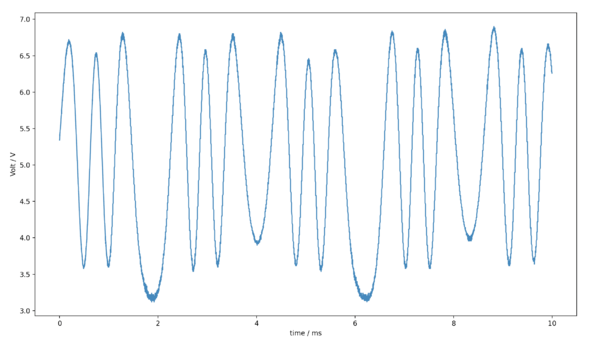
After the alignment of the optical setup, we applied sinusoidal voltage to the transducer attached to the mirror tightly. intensity fluctuation is recorded by the homemade photodiode. Data from the photodiode is collected by the oscilloscope. The typical figure from the oscilloscope is shown in Figure 7. According to the equation mentioned before, the number of peaks during each period corresponds to the radio of displacement and laser wavelength. In this case, we can measure the displacement for various frequencies. The frequency range is from 86 Hz to 130 Hz.

Figure 7A: The display on the oscilloscope at $f=103Hz$. After applying the voltage to the transducer, the voltage output from photodiode changes with time.

Figure 7B: The display on the oscilloscope at $f=116Hz$. After applying the voltage to the transducer, the voltage output from photodiode changes with time.

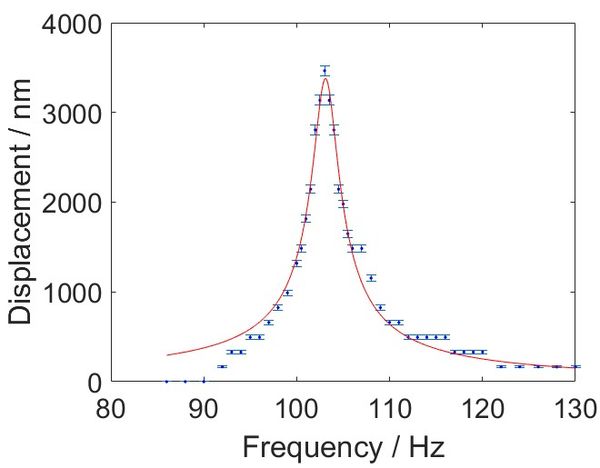
We plot the displacement for different frequencies with the errorbar in Figure 6. Uncertainty is the square root uncertainty of the count number. For a driven, damped, and harmonic oscillator, the relation between displacement and frequency is

$|A|={\frac {f_{0}}{\sqrt {\left(\omega _{0}^{2}-\omega ^{2}\right)^{2}+4\beta ^{2}\omega ^{2}}}}$

Where $f_{0}$ is the amplitude, $\omega _{0}$ is the resonance frequency, and $\beta _{0}$ is a constant. With this equation, we can fit the frequency response curve. Because there is only one peak or valley for a frequency lower than 92 Hz or higher than 120 Hz, and the error is significant and non-negligible. We exclude those in the fitting process. Finally, the fitting root mean squared error (RMSE) is 130.38. Fitted $\beta$ is $1.3\pm 0.2$. The fitting resonance frequency $\omega _{0}$ is $103.1\pm 0.1Hz$.

Figure 8: Frequency response curve for the transducer system with errorbar. The blue dots represent the displacement measured with different frequencies. Error bars are the square root uncertainty. Red line is the fitting curve for a driven, damped, harmonic oscillator.

Discussion

In figure 7A, we could see that the nearest you are to the natural resonance frequency of the system, the response of the system to the driven force will coupled and the number of oscillation increase. Meanwhile, in figure 7B the number of oscillations is lower. These phenomena is in concordance with the relation for $|A|$, in the past section.

Our final result fits our data to the best Lorentzian function. When we say best, we talk about the function with the lowest Root Mean Square Error (RMSE).

RMSE is defined as follow:

$\operatorname {RMSE} ={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}(A_{i}-{\hat {A_{i}}})^{2}}}$

where $A_{i}$ is the measured displacement and ${\hat {A_{i}}}$ is the predicted displacement by the function model. The core of this method is to calculate the distance between the measured and predicted values and take the root mean of them.

The displacements ($A_{i}$) we have measured are in the regimen of thousands and the error is ~100. This is attributed to the response of the system to lower and higher frequencies, from the resonance frequency, were we could see they stick together. For near resonance, the model fits pretty well and the fitting method provides a resonance frequency $103.1Hz$.

Finally, we believe that most of the errors in this experiment came from the fact that the laser diode is a homemade laser diode so it does not have a good temperature control. Moreover, the homemade laser diode holder is not tightly fit to the laser diode collimation tube which can cause displacement of the laser beam.

Conclusion

We have shown indeed that we can characterize the resonance frequency of a system. For this particular application, we could see a resonance frequency of $103Hz$ for the system transducer plus mirror. This could be improve by temperature stabilisation of the laser diode. Finally, this technique has a great potential to be used in initial experimental laboratories due his simplicity to illustrates concepts such as interference and driven oscillator, which are important in advance physics modules.

References

[1] Freschi, A. A., et al. "Laser interferometric characterization of a vibrating speaker system." American Journal of Physics 71.11 (2003): 1121-1126. https://doi.org/10.1119/1.1586262

[2] Skarha, Matthew. "Laser interferometric characterization for a vibrating speaker system." http://mattskarha.com/assets/docs/Laser%20interferometric%20characterization%20for%20a%20vibrating%20speaker%20system%20good.pdf

[3] Pathare, Shirish, and Vikrant Kurmude. "Low cost Michelson–Morley interferometer." Physics Education 51.6 (2016): 063001. https://doi.org/10.1088/0031-9120/51/6/063001