Quantum Random Number Generator: Difference between revisions
| (266 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
== Team Members == | == '''Team Members''' == | ||
Wang Yang A0228753X | Wang Yang A0228753X | ||
| Line 6: | Line 6: | ||
Zhang Munan A0236273E | Zhang Munan A0236273E | ||
== Idea == | == '''Idea''' == | ||
We live in an increasingly connected world, where a superior source of entropy is the key to data security. The effectiveness of any cryptographic system is determined by the strength of the keys it used. In turn, the strength of the key is determined by the degree of randomness used in its generation. | We live in an increasingly connected world, where a superior source of entropy is the key to data security. The effectiveness of any cryptographic system is determined by the strength of the keys it used. In turn, the strength of the key is determined by the degree of randomness used in its generation. Besides, large amount of random numbers are at the core of Monte Carlo simulations, which are widely used in scientific research. Methods produce random numbers from any algorithm are called pseudo-random number generator(PRNG). And random numbers generated by PRNG are deterministic by definition and therefore unsuitable for cryptographic purposes. | ||
In order to generate unpredictable random numbers, hardware random number generators have been widely used. These physically generated random numbers are considered "truly" random because it is either practically or fundamentally impossible to predict the outcome of such a device. Quantum Random Number Generators (QRNGs) belong to a class of hardware random number generators and leverage the random properties of quantum physics to generate a true source of entropy, improving the quality of seed content for key generation. | |||
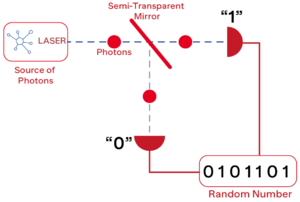
Early QRNGs were based on radioactive decay. And more recently, QRNGs based on Poisson statistics of photons have been developed. The core idea is shown in the figure below. Single photons generated by a laser source are incident on a semi-transparent mirror and the mutually exclusive events (reflection/transmission) are detected and associated with ‘0’ or ‘1’ bit values respectively. The unpredictability of generated numbers is ensured by the quantum nature of the process. However, such a scheme needs a reliable single photon source as well as single photon detectors and it's not possible for our project. Here, we decided to build a QRNG based on measuring vacuum fluctuations of a light field as a random source. More details will be discussed in the principle part. | |||
[[File:Principle schematic of QRNG.png|thumb|300px|'''Figure 1. Schematic of branching path quantum random number generators''']] | |||
=== Benefits of having a quantum random number generator === | |||
* The source of randomness is unpredictable and controlled by quantum process. | |||
* Live/real-time monitoring of entropy source is possible and highly effective as well. | |||
* All attacks on the entropy source are detectable. | |||
== | === Application of quantum random number generator === | ||
* Securing data at rest in data centres | |||
* Securing any kind of sensitive data | |||
* Securing data in the cloud | |||
* One-time pad for authentication in banking and other transactions | |||
* Gaming applications and lottery | |||
* Block-chain network | |||
* Numerical simulations, statistical research | |||
* IoT devices | |||
* E-commerce and banking applications | |||
* Cryptographic applications | |||
* Telecom and 5G | |||
* Monte Carlo Simulation | |||
== '''Principles''' == | |||
[[File:Schematic of setup 2.png|thumb|300px|'''Figure 2. Schematic of setup''']] | |||
Figure 2 schematically shows our setup. Such a setup is known as balanced homodyne detection and can extract the information of the electrical field in the second mode entering the polarizing beam-splitter (PBS) by measuring the photocurrent difference <math>i_1-i_2</math>. A continuous wave laser (wavelength 658 nm) is incident on one input port of the PBS and used as the local oscillator (LO), while another input port is empty. So the homodyne detection is trying to measure the vacuum state of the electromagnetic field. The randomness source in our setup is the fluctuations of the vacuum field. Here we tried to balance the optical power impinging on the two photodiodes, therefore any power fluctuation coming from the laser diode will be detected simultaneously and canceled in the photocurrent difference. | |||
Alternatively, the randomness can be seen as coming from the shot noise of the photocurrents <math>i_1</math> and <math>i_2</math> with a power proportional to the average optical power. Since the shot noise currents from the diodes are uncorrelated, the y add up. And the amplitude fluctuations in the laser intensity (referred to as classical noise) can be eliminated by measuring the photocurrent difference. | |||
== '''Setup''' == | |||
The practical setup (shown in Figure 3) was built with as few components as possible to create a baseline performance that we can compare. | |||
[[File:Experimental setup.png|thumb|300px|'''Figure 3. Experimental setup''']] | |||
[[File:Experimental setup.png|thumb|300px| | |||
''' | |||
== | ==='''Tool list'''=== | ||
* 26 February 2022: | ① Laser Diode | ||
<gallery widths= | : Laser Diode is powered by a laser driving unit. The light intensity can be changed by changing the laser current. | ||
File:Basic characterization of photodiode test.jpeg|'''Basic characterization of photodiode | ② Focal Lens | ||
File:Schematic of basic characterization of photodiode test.png|'''Schematic of basic characterization of photodiode | : By adjusting the focal lens, the intensity of light that finally hits the photodiodes is adjusted. | ||
③ RP: Rotatable Polarizer | |||
: The polarization state of the light is adjusted by rotating the polarizer. | |||
④ Mirror 1 | |||
: By adjusting mirror 1, the position of transmitted and reflected light spots hitting on PD1 and PD2 can be adjusted simultaneously. | |||
⑤ PBS: Polarizing Beam Splitter | |||
: The laser beam incident on the PBS can pass through or be reflected depending on the polarization state. If the incident beam is diagonal polarized (45°), the intensity of reflected and transmitted light is equal. | |||
⑥ Mirror 2 | |||
: By adjusting mirror 2, the position of transmitted light spots hitting on PD2 can be tuned. | |||
⑦&⑧ Photodiodes | |||
: Detect the intensity of incident light. | |||
⑩ Gain block | |||
:A ready-made 60 dB gain Block from quantum optic lab. | |||
⑪ High pass filter | |||
:Designed cutoff frequency = 60 MHz. | |||
==='''Description'''=== | |||
The total light power is changed by changing the laser current and adjusting the focal lens, while the power of the two output ports of the PBS is balanced by rotating the polarizer in front of the laser diode. Light leaving the PBS is detected by a pair of reverse-biased photodiodes connected in series to perform the current subtraction. By adjusting the orientation of M1 and M2, the light intensity incident on PD1 and PD2 can be adjusted and balanced. The balancing of the photocurrents is monitored by observing the voltage drop across a resister <math>R_{DC}</math> (DC port). Here we use a multimeter to measure the voltage. The fluctuations <math>\Delta(i_1-i_2)</math> are amplified by a 60 dB ready-made Gain block. And after that, a high pass filter (HPF) with a cutoff frequency of 60 MHz is used to filter out low frequency noise. | |||
==='''Characterization list'''=== | |||
① Oscilloscope: Used to monitor the AC port and collect data. | |||
② Spectrum Analyzer: Used to analyze the spectrum of total noise. | |||
③ Multimeter:Used to monitor the DC port and balance two photodiodes. | |||
== '''Process''' == | |||
* '''26 February 2022:''' | |||
* Did a basic characterization of photodiode | |||
* Inputted a sine wave signal and a laser pointer light, observed the waveform of the photodiode | |||
<gallery widths=300px heights=200px> | |||
File:Basic characterization of photodiode test.jpeg|'''Figure 4. Basic characterization of photodiode''' | |||
File:Schematic of basic characterization of photodiode test.png|'''Figure 5. Schematic of basic characterization of photodiode''' | |||
</gallery> | </gallery> | ||
* 5 March 2022: | |||
<gallery widths= | :To understand the frequency response of the circuit shown in figure 5, we use a function generator to generate a sinusoidal signal to drive the LED, and use this circuit to measure the light output. When the frequency of the signal is low, we can see a relatively complete sine waveform on the oscilloscope. But when the frequency exceeds 1GHz, we could not observe a regular and stable waveform. | ||
File: | * '''5 March 2022:''' | ||
* Used different resistors to test the frequency response of photodiode | |||
<gallery widths=300px heights=200px> | |||
File:Frequency of PD.png|'''Figure 6. Graph of the frequency response of photodiode''' | |||
</gallery> | </gallery> | ||
* 12 March 2022: | :We changed the resistors in Figure 6, from 1 kΩ to 11 kΩ and then 20 kΩ. We found that the higher the resistance of the resistor, the larger the output voltage but less sensitive to the high frequency. That is because a reverse-biased photodiode has a certain capacitance and forms an RC series circuit with the resistor. The larger the resistor, the larger the time constant <math>\tau=RC</math> of the RC circuit, and the slower the charge and discharge, which leads to a worse response to high frequency signals. | ||
* Build up the laser system | * '''12 March 2022:''' | ||
* Build up the laser system and ensured the laser output | |||
<gallery widths= | <gallery widths=300px heights=200px> | ||
File:Laser diode.png| | File:Laser diode.png|'''Figure 7. HL6501MG laser diode and schematic of internal circuit''' | ||
File:Schematic of electronics laserconnector circuit.jpeg|'''Schematic of electronics | File:Schematic of electronics laserconnector circuit.jpeg|'''Figure 8. Schematic of electronics laser connector circuit''' | ||
File:Laser source setup.png|'''Figure 9. Laser source setup''' | |||
</gallery> | </gallery> | ||
* 19 March 2022: | :We used an HL6501MG laser diode, which is a 0.65 μm band AlGaInP laser diode (LD) with a multi-quantum well (MQW) structure. It is suitable as a light source for large-capacity optical disc memories and various other types of optical equipment. Hermetic sealing of the small package (φ=5.6 mm) assures high reliability. | ||
<gallery widths= | |||
File:Photo diode outlines.png| | :The Laser source consists of ① Laser diode; ② Thermostat; ③ Supply circuit for Laser diode and Thermostat; ④ Shell; ⑤ Focal lens; ⑥ Radiator. The Laser Diode is in the thermostat which is connected to the Radiator. We can set the temperature on the Laser power supply. The Thermostat and Radiator will keep the temperature of the laser diode as same as that set on the laser power supply. There is a focal lens in front of the laser diode. We can use it to change the focal length the enlarge the laser intensity hitting on the photodiodes. And a shell made of acrylic sheet and 4 balance posts. | ||
File:Principle of photodiode driving circuit.png|'''Principle of photodiode driving circuit''' | * '''19 March 2022:''' | ||
File:Schematic photodiode driving circuit bolck.jpeg|'''Schematic photodiode driving circuit | * Soldered photodiode driving circuit | ||
* Test the feasibility | |||
<gallery widths=300px heights=200px> | |||
File:Photo diode outlines.png|'''Figure 10. S5972 Si PIN photodiode and schematic of internal circuit''' | |||
File:Principle of photodiode driving circuit.png|'''Figure 11. Principle of photodiode driving circuit''' | |||
File:Schematic photodiode driving circuit bolck.jpeg|'''Figure 12. Schematic photodiode driving circuit block''' | |||
</gallery> | </gallery> | ||
:We used an S5972 high-speed Si PIN photodiode to detect the light, which is designed for visible to near-infrared light detection. These photodiodes provide wideband characteristics at a low bias, making them suitable for optical communications and other high-speed photometry. | |||
* 26 March 2022: | |||
:We soldered all the components on the circuit chip as Figure 11 shows. After that, we tested its performance using a laser, it was approved that the optical signal was converted into the electrical signal and was measured by the oscilloscope. | |||
* '''26 March 2022:''' | |||
* Build up the whole system | * Build up the whole system | ||
* Tune the bias of two photodiodes | * Tune the bias of two photodiodes | ||
<gallery widths=300px heights=200px> | |||
File:Whole setup.jpeg|'''Figure 13. The whole system setup''' | |||
</gallery> | |||
:We built up the whole setup on the optical platform. Then we tuned the bias of two photodiodes to make sure that the intensity of the laser hitting on both photodiodes is the same by adjusting the multimeter's voltage to around 0. | |||
* '''2 April 2022:''' | |||
* Focus the laser output | |||
* Maximize the laser power output | |||
* Characterize varaiation by varying optical power | |||
<gallery widths=300px heights=200px> | |||
File:Maximize the laser power output.jpeg|'''Figure 14. Maximize the laser power output''' | |||
File:The detector noise power by varying the incident optical power.jpg|'''Figure 15. The plot of the detector noise power by varying the incident optical power''' | |||
</gallery> | |||
:We found that the laser output power in front of the polarizer was about 20 mW, but the power detected by each photodiode was only 0.4 mW. That is because the spot size of the laser was relatively large compared with the detection area of the photodiode. Therefore we needed to focus the lens in the laser block to maximize the detected laser power. To do this, we blocked one photodiode and used a multimeter to monitor the light power detected by another photodiode. After trials, we got a maximum value of voltage drop of 9.17 V, which corresponds to an optical power of 2.08 mW on each photodiode. | |||
:Then, we characterized the change of noise level while rising incident optical power. And then we plotted a graph as shown in Figure 15, it is easy to find when the optical power is in a relatively low range, the noise level is flat which corresponds to the horizontal red line. While the optical power rises, the noise level increases with the optical power in a proportional manner. Therefore, we have enough reasons to believe that the overall noise is dominated by electronic noise in the low optical power range, while the noise level is dominated by shot noise in the high optical power range. | |||
* '''9 April 2022:''' | |||
* 9 April 2022: | * Soldered high pass filter | ||
* Test its feasibility | |||
<gallery widths=300px heights=200px> | |||
* | File:Highpass filter principle circuit.png|'''Figure 16. Schematic of high pass filter circuit''' | ||
<gallery widths= | File:Graph of theoretical high pass filter frequency response.jpg.png|'''Figure 17. Graph of theoretical high pass filter frequency response''' | ||
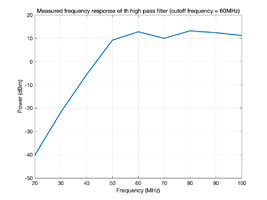
File: | File:Frequency of HPF.png|'''Figure 18. Graph of measured high pass filter frequency response''' | ||
File: | File:Schematic of high pass filter.jpeg|'''Figure 19. Setup of high pass filter''' | ||
File:Graph of measured high pass filter frequency response. | File:Setup of gain block and high pass filter.jpeg|'''Figure 20. Setup of gain block and high pass filter''' | ||
File: | |||
</gallery> | </gallery> | ||
:The measured total noise has a lot of low-frequency noise and is relatively flat power density in the range of 60-200 MHz. With a low pass filter of 200 MHz in the oscilloscope, we just needed a high pass filter of 60 MHz which compresses the low-frequency fluctuations. So we designed a high pass filter of 60 MHz and soldered the high pass filter. | |||
:After that, we tested its performance. By comparing with the theoretical high pass filter graph, the measured high pass filter frequency response showed a high correspondence with it, which means it is feasible to apply it to the whole system to suppress the low-frequency fluctuations. | |||
* '''16 April 2022:''' | |||
* Apply the high pass filter to the circuit and test | |||
* Record data and draw some graphs analysis | |||
: In order to verify that the signals we obtained were quantum random numbers, we recorded the data at different sampling rates and performed autocorrelation calculations. These can be found in the "Result"-"Autocorrelation" part. | |||
* 23 April 2022: | * '''23 April 2022:''' | ||
* Processing experimental data | * Processing experimental data | ||
* Draw autocorrelation images | * Draw autocorrelation images | ||
* Summarize and upload the experimental results | * Summarize and upload the experimental results | ||
== | == '''Results''' == | ||
[1] | ==='''Quantum noise'''=== | ||
To ensure that the fluctuations at the amplifier output are dominated by quantum noise, the spectral power density is measured (in Figure 21. ). | |||
[[File:Amplified noise levels measured into a resolution bandwidth B = 3 MHz..jpg|thumb|500px|center|'''Figure 21. Schematic of branching path quantum random number generators''']] | |||
Amplified noise levels are measured into a resolution bandwidth B = 3 MHz. The total noise is measured from the photocurrent difference <math>i_1-i_2</math> with equal optical power impinging on both photodiodes. The current <math>i_1</math> of a single photodiode reveals colored classical noise. The electronic noise is measured without any optical input. | |||
In an alternative view, the laser beam can be seen as generating photocurrents <math>i_1</math> and <math>i_2</math> with a shot noise power proportional to the average optical power. The shot noise currents from the diodes add up as they are uncorrelated, while amplitude fluctuations in the laser intensity (referred to as classical noise) do not affect the photocurrent difference. | |||
=== '''Autocorrelation'''=== | |||
Autocorrelation, sometimes known as serial correlation in the discrete-time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations as a function of the time lag between them. In our experiment, if we obtain an ideal '''quantum random number generator''', the autocorrelation will be 1 when the time lag is 0, while the autocorrelation will be close to 0 when the time lag is not 0. | |||
Given a signal <math>f(t)</math>, the continuous autocorrelation <math>R_{ff}(\tau)</math> is most often defined as the continuous cross-correlation integral of <math>f(t)</math> with itself, at lag <math>\tau</math>. | |||
:::::::::::::::::::<math>R_{ff}(\tau) = \int_{-\infty}^\infty f(t+\tau)\overline{f(t)}\, {\rm d}t = \int_{-\infty}^\infty f(t) \overline{f(t-\tau)}\, {\rm d}t</math> | |||
where <math>\overline{f(t)}</math> represents the complex conjugate of <math>f(t)</math>. Note that the parameter <math>t</math> in the integral is a dummy variable and is only necessary to calculate the integral. It has no specific meaning. | |||
*'''Experimental result''' | |||
:::<gallery widths=500px heights=300px> | |||
File:2.5 GHz (-20,20) After Highpass1.png|'''Figure 22. Autocorrelation of the total noise signal sampled at 2.5 GHz''' | |||
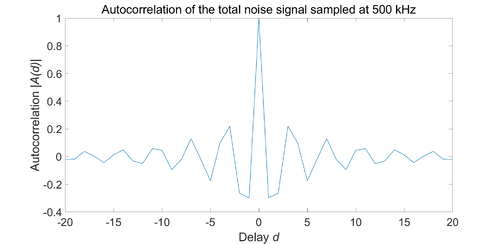
File:500 kHz (-20,20) After Highpass1.png|'''Figure 23. Autocorrelation of the total noise signal sampled at 500 KHz''' | |||
:::</gallery> | |||
We recorded several sets of data with different sampling frequencies (2.5 GHz to 500 kHz) and obtained autocorrelation for each group. A very high correlation between any two adjacent points was observed when we use a 2.5 GHz sampling rate. This is simply because of an extremely high sampling rate which results in every two adjacent points being almost at the same position. We can get a better correlation by reducing the sampling frequency to such as 10 MHz or even lower. | |||
But the autocorrelation with a 500 kHz sampling rate is still not ideal. This is limited by our experimental setup. We caught up with too much electronic interference. A well-designed experimental setup with integrated photodiodes, amplifier, and high pass filter will stimulate a better result. | |||
=== '''Randomness Extraction'''=== | |||
The amplified total noise is digitized into 16-bit words at a sampling rate of 10 MHz (because we get the best autocorrelation result at this sampling rate) and recorded in binary form by an oscilloscope. All data are discrete values between <math>-2^{15}</math> and <math>2^{15}-1</math>. Figure 24 below shows the distribution of our raw data, which fits a Gaussian distribution with a standard deviation <math>\sigma = 5240</math>. | |||
[[File:Raw_data.png|thumb|500px|center|'''Figure 24. Distribution of row data and fitted with Gaussian distribution.''']] | |||
In many applications, however, random numbers are required to be not only unpredictable but also uniformly distributed. Therefore the raw data collected by the oscilloscope cannot be used directly. Various randomness extractors, such as Trevisan's extractor and Linear Feedback Shift Register, have been used to convert non-uniformly distributed raw data into a uniformly distributed binary stream. For simplicity, here we used random matrix multiplications to extract uniformly distributed random numbers. | |||
[[File:WechatIMG18990.jpeg|frameless|350px|center]] | |||
The equation above shows how it works. Since our raw data is recorded in binary form, it is an N-row column vector <math>r_i</math> with all elements 0 or 1. And the <math>M \times N</math> binary matrix is an algorithmically generated pseudo-random matrix. Then the raw data and the random matrix are multiplied (binary OR and XOR) to produce a column vector <math>s_i</math> of M rows. As long as the size of the random matrix is large enough, 0 and 1 in the output <math>s_i</math> will be almost uniformly distributed. Here M can take any integer not greater than N. The reason is that the voltage at AC port fluctuates around 0 V and the first few bits in each binary number are typically unused (all 0). Therefore the entropy in the raw data is smaller than the size of the data (e.g.6 bits of entropy per 8 bits sample). The standard approach would be to first estimate the entropy in the raw data and then choose the value of N to extract the randomness. Since in our project, we didn't do that, here we choose N = M. | |||
[[File:Extracted.png|thumb|500px|center|'''Figure 25, Distribution of random data after the random matrix multiplication.''']] | |||
Figure 25 shows the distribution of the data after randomness extraction. As we can see, all data fall within the <math>\pm3\sigma</math> bounds, so we have reason to believe that extracted data is almost uniformly distributed. | |||
[[File:Contrast.png||thumb|500px|center|'''Figure 26. Distribution of random numbers before (blue) and after (red) the randomness extraction, shown in time domain (left) and histogram (right)''']] | |||
Figure 26 shows the comparison between random numbers before and after the randomness extraction. | |||
=== '''Randomness Test'''=== | |||
To verify the randomness of the experimental results we obtained, we used two compression protocols(rar and zip) to compress the random numbers we generated. The compressed file size does not change significantly compared with the original file(from 58k to 55k), which, to some extent, illustrates the randomness of our results. | |||
== '''Acknowledgement''' == | |||
It is an extremely thing and a big challenge for us to conduct this experiment, during this process, we encountered a lot of problems and solved them one by one with others' help. So we want to show our appreciation to these people. | |||
First and foremost, we would like to express our deepest appreciation to Prof Christian Kurtsiefer. Thanks to his kind help to get some gadgets for this project, we have done a lot of work with his insightful ideas and suggestions. | |||
Then, we are also extremely grateful to Dr. Shi Yicheng, we feel very impressed and lucky for his kindness when we were doing this project with his help. Whatever we need or wherever we need to go, he always gives us very clear guidance and does us a standard demonstration to help us understand. His quick feedback and helpful guidance give us a deep impression and let us move forward. Sincerely, we want to say thank him very much again and give him best wishes for his next study period in the United States. | |||
At last, we would like to offer our gratitude to each other in our team. It is we that insist on and try constantly, and we can finally get an achieved result. This camaraderie is the best thing we got than the experimental result. | |||
== '''References''' == | |||
[1] Miguel Herrero-Collantes and Juan Carlos Garcia-Escartin, Quantum random number generators, Rev. Mod. Phys, 89, 015004. | |||
[2] Shi, Yicheng, Brenda Chng, and Christian Kurtsiefer, Random numbers from vacuum fluctuations, Applied Physics Letters, 109.4 (2016): 041101. | |||
[3] https://www.digchip.com/datasheets/parts/datasheet/625/HL6501MG-pdf.php | |||
[4] https://www.farnell.com/datasheets/3171163.pdf | |||
Latest revision as of 17:52, 29 April 2022
Team Members
Wang Yang A0228753X
Xiao Yucan A0236278W
Zhang Munan A0236273E
Idea
We live in an increasingly connected world, where a superior source of entropy is the key to data security. The effectiveness of any cryptographic system is determined by the strength of the keys it used. In turn, the strength of the key is determined by the degree of randomness used in its generation. Besides, large amount of random numbers are at the core of Monte Carlo simulations, which are widely used in scientific research. Methods produce random numbers from any algorithm are called pseudo-random number generator(PRNG). And random numbers generated by PRNG are deterministic by definition and therefore unsuitable for cryptographic purposes.
In order to generate unpredictable random numbers, hardware random number generators have been widely used. These physically generated random numbers are considered "truly" random because it is either practically or fundamentally impossible to predict the outcome of such a device. Quantum Random Number Generators (QRNGs) belong to a class of hardware random number generators and leverage the random properties of quantum physics to generate a true source of entropy, improving the quality of seed content for key generation.
Early QRNGs were based on radioactive decay. And more recently, QRNGs based on Poisson statistics of photons have been developed. The core idea is shown in the figure below. Single photons generated by a laser source are incident on a semi-transparent mirror and the mutually exclusive events (reflection/transmission) are detected and associated with ‘0’ or ‘1’ bit values respectively. The unpredictability of generated numbers is ensured by the quantum nature of the process. However, such a scheme needs a reliable single photon source as well as single photon detectors and it's not possible for our project. Here, we decided to build a QRNG based on measuring vacuum fluctuations of a light field as a random source. More details will be discussed in the principle part.
Benefits of having a quantum random number generator
- The source of randomness is unpredictable and controlled by quantum process.
- Live/real-time monitoring of entropy source is possible and highly effective as well.
- All attacks on the entropy source are detectable.
Application of quantum random number generator
- Securing data at rest in data centres
- Securing any kind of sensitive data
- Securing data in the cloud
- One-time pad for authentication in banking and other transactions
- Gaming applications and lottery
- Block-chain network
- Numerical simulations, statistical research
- IoT devices
- E-commerce and banking applications
- Cryptographic applications
- Telecom and 5G
- Monte Carlo Simulation
Principles

Figure 2 schematically shows our setup. Such a setup is known as balanced homodyne detection and can extract the information of the electrical field in the second mode entering the polarizing beam-splitter (PBS) by measuring the photocurrent difference . A continuous wave laser (wavelength 658 nm) is incident on one input port of the PBS and used as the local oscillator (LO), while another input port is empty. So the homodyne detection is trying to measure the vacuum state of the electromagnetic field. The randomness source in our setup is the fluctuations of the vacuum field. Here we tried to balance the optical power impinging on the two photodiodes, therefore any power fluctuation coming from the laser diode will be detected simultaneously and canceled in the photocurrent difference.
Alternatively, the randomness can be seen as coming from the shot noise of the photocurrents and with a power proportional to the average optical power. Since the shot noise currents from the diodes are uncorrelated, the y add up. And the amplitude fluctuations in the laser intensity (referred to as classical noise) can be eliminated by measuring the photocurrent difference.
Setup
The practical setup (shown in Figure 3) was built with as few components as possible to create a baseline performance that we can compare.

Tool list
① Laser Diode
- Laser Diode is powered by a laser driving unit. The light intensity can be changed by changing the laser current.
② Focal Lens
- By adjusting the focal lens, the intensity of light that finally hits the photodiodes is adjusted.
③ RP: Rotatable Polarizer
- The polarization state of the light is adjusted by rotating the polarizer.
④ Mirror 1
- By adjusting mirror 1, the position of transmitted and reflected light spots hitting on PD1 and PD2 can be adjusted simultaneously.
⑤ PBS: Polarizing Beam Splitter
- The laser beam incident on the PBS can pass through or be reflected depending on the polarization state. If the incident beam is diagonal polarized (45°), the intensity of reflected and transmitted light is equal.
⑥ Mirror 2
- By adjusting mirror 2, the position of transmitted light spots hitting on PD2 can be tuned.
⑦&⑧ Photodiodes
- Detect the intensity of incident light.
⑩ Gain block
- A ready-made 60 dB gain Block from quantum optic lab.
⑪ High pass filter
- Designed cutoff frequency = 60 MHz.
Description
The total light power is changed by changing the laser current and adjusting the focal lens, while the power of the two output ports of the PBS is balanced by rotating the polarizer in front of the laser diode. Light leaving the PBS is detected by a pair of reverse-biased photodiodes connected in series to perform the current subtraction. By adjusting the orientation of M1 and M2, the light intensity incident on PD1 and PD2 can be adjusted and balanced. The balancing of the photocurrents is monitored by observing the voltage drop across a resister (DC port). Here we use a multimeter to measure the voltage. The fluctuations are amplified by a 60 dB ready-made Gain block. And after that, a high pass filter (HPF) with a cutoff frequency of 60 MHz is used to filter out low frequency noise.
Characterization list
① Oscilloscope: Used to monitor the AC port and collect data.
② Spectrum Analyzer: Used to analyze the spectrum of total noise.
③ Multimeter:Used to monitor the DC port and balance two photodiodes.
Process
- 26 February 2022:
* Did a basic characterization of photodiode * Inputted a sine wave signal and a laser pointer light, observed the waveform of the photodiode
-
Figure 4. Basic characterization of photodiode
-
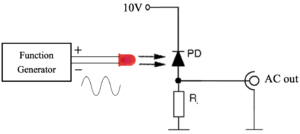
Figure 5. Schematic of basic characterization of photodiode
- To understand the frequency response of the circuit shown in figure 5, we use a function generator to generate a sinusoidal signal to drive the LED, and use this circuit to measure the light output. When the frequency of the signal is low, we can see a relatively complete sine waveform on the oscilloscope. But when the frequency exceeds 1GHz, we could not observe a regular and stable waveform.
- 5 March 2022:
* Used different resistors to test the frequency response of photodiode
-
Figure 6. Graph of the frequency response of photodiode
- We changed the resistors in Figure 6, from 1 kΩ to 11 kΩ and then 20 kΩ. We found that the higher the resistance of the resistor, the larger the output voltage but less sensitive to the high frequency. That is because a reverse-biased photodiode has a certain capacitance and forms an RC series circuit with the resistor. The larger the resistor, the larger the time constant of the RC circuit, and the slower the charge and discharge, which leads to a worse response to high frequency signals.
- 12 March 2022:
* Build up the laser system and ensured the laser output
-
Figure 7. HL6501MG laser diode and schematic of internal circuit
-
Figure 8. Schematic of electronics laser connector circuit
-
Figure 9. Laser source setup
- We used an HL6501MG laser diode, which is a 0.65 μm band AlGaInP laser diode (LD) with a multi-quantum well (MQW) structure. It is suitable as a light source for large-capacity optical disc memories and various other types of optical equipment. Hermetic sealing of the small package (φ=5.6 mm) assures high reliability.
- The Laser source consists of ① Laser diode; ② Thermostat; ③ Supply circuit for Laser diode and Thermostat; ④ Shell; ⑤ Focal lens; ⑥ Radiator. The Laser Diode is in the thermostat which is connected to the Radiator. We can set the temperature on the Laser power supply. The Thermostat and Radiator will keep the temperature of the laser diode as same as that set on the laser power supply. There is a focal lens in front of the laser diode. We can use it to change the focal length the enlarge the laser intensity hitting on the photodiodes. And a shell made of acrylic sheet and 4 balance posts.
- 19 March 2022:
* Soldered photodiode driving circuit * Test the feasibility
-
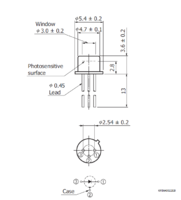
Figure 10. S5972 Si PIN photodiode and schematic of internal circuit
-
Figure 11. Principle of photodiode driving circuit
-
Figure 12. Schematic photodiode driving circuit block
- We used an S5972 high-speed Si PIN photodiode to detect the light, which is designed for visible to near-infrared light detection. These photodiodes provide wideband characteristics at a low bias, making them suitable for optical communications and other high-speed photometry.
- We soldered all the components on the circuit chip as Figure 11 shows. After that, we tested its performance using a laser, it was approved that the optical signal was converted into the electrical signal and was measured by the oscilloscope.
- 26 March 2022:
* Build up the whole system * Tune the bias of two photodiodes
-
Figure 13. The whole system setup
- We built up the whole setup on the optical platform. Then we tuned the bias of two photodiodes to make sure that the intensity of the laser hitting on both photodiodes is the same by adjusting the multimeter's voltage to around 0.
- 2 April 2022:
* Focus the laser output * Maximize the laser power output * Characterize varaiation by varying optical power
-
Figure 14. Maximize the laser power output
-
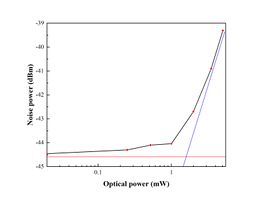
Figure 15. The plot of the detector noise power by varying the incident optical power
- We found that the laser output power in front of the polarizer was about 20 mW, but the power detected by each photodiode was only 0.4 mW. That is because the spot size of the laser was relatively large compared with the detection area of the photodiode. Therefore we needed to focus the lens in the laser block to maximize the detected laser power. To do this, we blocked one photodiode and used a multimeter to monitor the light power detected by another photodiode. After trials, we got a maximum value of voltage drop of 9.17 V, which corresponds to an optical power of 2.08 mW on each photodiode.
- Then, we characterized the change of noise level while rising incident optical power. And then we plotted a graph as shown in Figure 15, it is easy to find when the optical power is in a relatively low range, the noise level is flat which corresponds to the horizontal red line. While the optical power rises, the noise level increases with the optical power in a proportional manner. Therefore, we have enough reasons to believe that the overall noise is dominated by electronic noise in the low optical power range, while the noise level is dominated by shot noise in the high optical power range.
- 9 April 2022:
* Soldered high pass filter * Test its feasibility
-
Figure 16. Schematic of high pass filter circuit
-
Figure 17. Graph of theoretical high pass filter frequency response
-
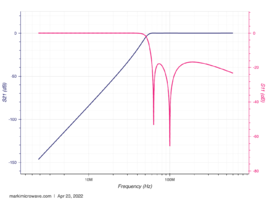
Figure 18. Graph of measured high pass filter frequency response
-
Figure 19. Setup of high pass filter
-
Figure 20. Setup of gain block and high pass filter
- The measured total noise has a lot of low-frequency noise and is relatively flat power density in the range of 60-200 MHz. With a low pass filter of 200 MHz in the oscilloscope, we just needed a high pass filter of 60 MHz which compresses the low-frequency fluctuations. So we designed a high pass filter of 60 MHz and soldered the high pass filter.
- After that, we tested its performance. By comparing with the theoretical high pass filter graph, the measured high pass filter frequency response showed a high correspondence with it, which means it is feasible to apply it to the whole system to suppress the low-frequency fluctuations.
- 16 April 2022:
* Apply the high pass filter to the circuit and test * Record data and draw some graphs analysis
- In order to verify that the signals we obtained were quantum random numbers, we recorded the data at different sampling rates and performed autocorrelation calculations. These can be found in the "Result"-"Autocorrelation" part.
- 23 April 2022:
* Processing experimental data * Draw autocorrelation images * Summarize and upload the experimental results
Results
Quantum noise
To ensure that the fluctuations at the amplifier output are dominated by quantum noise, the spectral power density is measured (in Figure 21. ).

Amplified noise levels are measured into a resolution bandwidth B = 3 MHz. The total noise is measured from the photocurrent difference with equal optical power impinging on both photodiodes. The current of a single photodiode reveals colored classical noise. The electronic noise is measured without any optical input. In an alternative view, the laser beam can be seen as generating photocurrents and with a shot noise power proportional to the average optical power. The shot noise currents from the diodes add up as they are uncorrelated, while amplitude fluctuations in the laser intensity (referred to as classical noise) do not affect the photocurrent difference.
Autocorrelation
Autocorrelation, sometimes known as serial correlation in the discrete-time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations as a function of the time lag between them. In our experiment, if we obtain an ideal quantum random number generator, the autocorrelation will be 1 when the time lag is 0, while the autocorrelation will be close to 0 when the time lag is not 0.
Given a signal , the continuous autocorrelation is most often defined as the continuous cross-correlation integral of with itself, at lag .
where represents the complex conjugate of . Note that the parameter in the integral is a dummy variable and is only necessary to calculate the integral. It has no specific meaning.
- Experimental result
We recorded several sets of data with different sampling frequencies (2.5 GHz to 500 kHz) and obtained autocorrelation for each group. A very high correlation between any two adjacent points was observed when we use a 2.5 GHz sampling rate. This is simply because of an extremely high sampling rate which results in every two adjacent points being almost at the same position. We can get a better correlation by reducing the sampling frequency to such as 10 MHz or even lower.
But the autocorrelation with a 500 kHz sampling rate is still not ideal. This is limited by our experimental setup. We caught up with too much electronic interference. A well-designed experimental setup with integrated photodiodes, amplifier, and high pass filter will stimulate a better result.
Randomness Extraction
The amplified total noise is digitized into 16-bit words at a sampling rate of 10 MHz (because we get the best autocorrelation result at this sampling rate) and recorded in binary form by an oscilloscope. All data are discrete values between and . Figure 24 below shows the distribution of our raw data, which fits a Gaussian distribution with a standard deviation .

In many applications, however, random numbers are required to be not only unpredictable but also uniformly distributed. Therefore the raw data collected by the oscilloscope cannot be used directly. Various randomness extractors, such as Trevisan's extractor and Linear Feedback Shift Register, have been used to convert non-uniformly distributed raw data into a uniformly distributed binary stream. For simplicity, here we used random matrix multiplications to extract uniformly distributed random numbers.
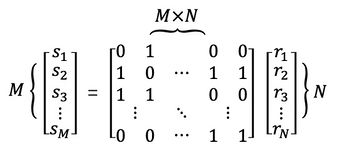
The equation above shows how it works. Since our raw data is recorded in binary form, it is an N-row column vector with all elements 0 or 1. And the binary matrix is an algorithmically generated pseudo-random matrix. Then the raw data and the random matrix are multiplied (binary OR and XOR) to produce a column vector of M rows. As long as the size of the random matrix is large enough, 0 and 1 in the output will be almost uniformly distributed. Here M can take any integer not greater than N. The reason is that the voltage at AC port fluctuates around 0 V and the first few bits in each binary number are typically unused (all 0). Therefore the entropy in the raw data is smaller than the size of the data (e.g.6 bits of entropy per 8 bits sample). The standard approach would be to first estimate the entropy in the raw data and then choose the value of N to extract the randomness. Since in our project, we didn't do that, here we choose N = M.
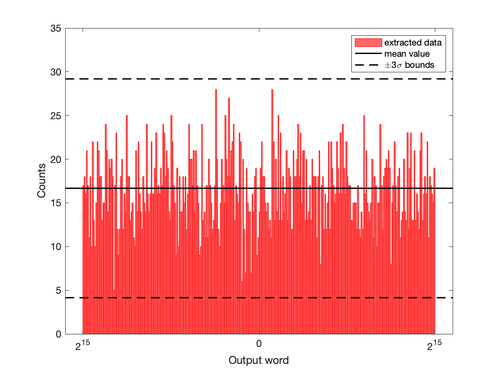
Figure 25 shows the distribution of the data after randomness extraction. As we can see, all data fall within the bounds, so we have reason to believe that extracted data is almost uniformly distributed.
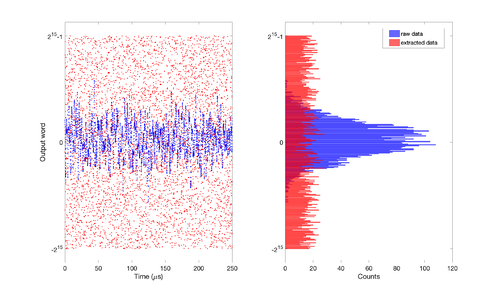
Figure 26 shows the comparison between random numbers before and after the randomness extraction.
Randomness Test
To verify the randomness of the experimental results we obtained, we used two compression protocols(rar and zip) to compress the random numbers we generated. The compressed file size does not change significantly compared with the original file(from 58k to 55k), which, to some extent, illustrates the randomness of our results.
Acknowledgement
It is an extremely thing and a big challenge for us to conduct this experiment, during this process, we encountered a lot of problems and solved them one by one with others' help. So we want to show our appreciation to these people.
First and foremost, we would like to express our deepest appreciation to Prof Christian Kurtsiefer. Thanks to his kind help to get some gadgets for this project, we have done a lot of work with his insightful ideas and suggestions.
Then, we are also extremely grateful to Dr. Shi Yicheng, we feel very impressed and lucky for his kindness when we were doing this project with his help. Whatever we need or wherever we need to go, he always gives us very clear guidance and does us a standard demonstration to help us understand. His quick feedback and helpful guidance give us a deep impression and let us move forward. Sincerely, we want to say thank him very much again and give him best wishes for his next study period in the United States.
At last, we would like to offer our gratitude to each other in our team. It is we that insist on and try constantly, and we can finally get an achieved result. This camaraderie is the best thing we got than the experimental result.
References
[1] Miguel Herrero-Collantes and Juan Carlos Garcia-Escartin, Quantum random number generators, Rev. Mod. Phys, 89, 015004.
[2] Shi, Yicheng, Brenda Chng, and Christian Kurtsiefer, Random numbers from vacuum fluctuations, Applied Physics Letters, 109.4 (2016): 041101.
[3] https://www.digchip.com/datasheets/parts/datasheet/625/HL6501MG-pdf.php