Laser Microphone

A laser spot illuminating a vibrating surface should move along with it, and tracking the motion of the spot should theoretically allow us to retrieve some of the information regarding the vibrations of the surface. If a loud enough sound causes the surface to vibrate, this should theoretically be enough for the transmission of audio information through visual means. The signal obtained will then be put through a few different digital signal processing techniques in an attempt to retrieve a (good enough) copy of the original audio.

The possible applications for such a device are already covered by existing mature technologies, but the idea of transmitting raw sound information "directly" via a laser without physical connections or converting the information into a different representation based on a special protocol (e.g. Wi-Fi or Bluetooth) is in itself an interesting curiosity. In this project, we will attempt to explore the effectiveness of a simple setup made of basic electronics found around the lab in recording audio without special circuitry, and also how digital signal processing techniques can help with improving the audio obtained.

Team Members

A0166927N | Marcus Low Zuo Wu

A0171267A | Nicholas Chong Jia Le

Methods and Requirements

Using a photodiode / array of photodiodes, we attempt to record audio by measuring the signal from a laser reflecting off a surface near the sound.

Due to the nature of the setup mentioned, we require a decently dim environment to minimise noise, a visible light laser (does not need to be high powered but needs to be decently collimated), an optical bench, a set of photodiodes that can detect the laser light and produce a signal, and an electronic setup that allows us to capture and export the signal from the photodiodes.

Background

Level (logarithmic quantity)

A power level is a logarithmic quantity used to measure power, power density or sometimes energy, with commonly used unit decibel (dB).

Power level

Level of a power quantity, denoted L_P, is defined by

$L_{P}={\frac {1}{2}}\log _{\mathrm {e} }\!\left({\frac {P}{P_{0}}}\right)\!~\mathrm {Np} =\log _{10}\!\left({\frac {P}{P_{0}}}\right)\!~\mathrm {B} =10\log _{10}\!\left({\frac {P}{P_{0}}}\right)\!~\mathrm {dB} .$

where

• P is the power quantity;
• P₀ is the reference value of P.

Field (or root-power) level

The level of a root-power quantity (also known as a field quantity), denoted L_F, is defined by

$L_{F}=\log _{\mathrm {e} }\!\left({\frac {F}{F_{0}}}\right)\!~\mathrm {Np} =2\log _{10}\!\left({\frac {F}{F_{0}}}\right)\!~\mathrm {B} =20\log _{10}\!\left({\frac {F}{F_{0}}}\right)\!~\mathrm {dB} .$

where

• F is the root-power quantity, proportional to the square root of power quantity;
• F₀ is the reference value of F.

Low-pass filter

First order passive low-pass filter (top) and second order passive low-pass filter (bottom) demonstrating how higher order filters can be obtained by chaining together lower order filters.

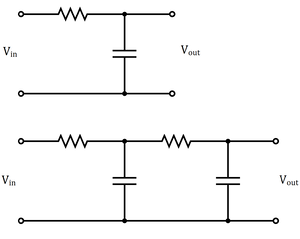
A low-pass filter is a filter that passes frequencies lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff. Low-pass filters provide a smoother form of a signal, removing the short-term fluctuations and leaving the longer-term trend.

Physical RC filter

The cutoff frequency of a passive first order low-pass filter is given by

$F={1 \over 2\pi RC}$

where $R$ is the value of the resistance and $C$ is the value of the capacitance.

The top circuit on the right shows a configuration that forms such a low-pass filter. As seen on the bottom circuit on the right, higher order passive filters can be made simply by chaining together lower order filters. One issue with using a physical filter is that it adds a load to the circuit, and for higher order filters, the final output signal has a greatly decreased magnitude compared to the pure signal obtained from the photodiode. This would require the addition of amplifiers to our circuit, increasing its complexity. Additionally, from observation, the noise introduced in the connection to the oscilloscope along with electrical noise picked up by the wires is significantly greater than the noise in the signal from the photodiode itself, making an external low-pass filter performing noise filtering on the photodiode output not very effective.

As such, digital signal processing will be done instead for noise filtering. Butterworth filters specifically will be used in this work in order to minimise distortion introduced into the input.

Butterworth Filter

The Butterworth filter is a signal processing filter that is designed to have a uniform sensitivity in the passband ("desired" frequencies), while having a sufficient rejection in the stopband ("unwanted" frequencies).

The (power) gain $G(f)$ of such a filter, with a cutoff frequency $f_{c}$ and filter order $n$ is given by:

$$G(f)={\frac {1}{1+\left({\frac {if}{if_{c}}}\right)^{2n}}}$$

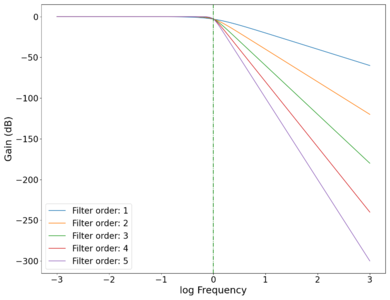
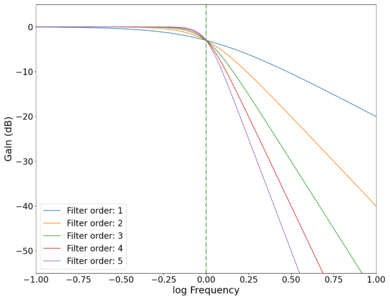
The gain curves for various orders of low-pass Butterworth filters are shown in the plot below, showing a roll-off of $-20n$ dB/decade of frequency. The roll-off at the cutoff frequency also gets sharper (roll-off starts closer to the cutoff frequency $f_{c}$ as opposed to slightly before $f_{c}$) as the order of the filter increases, as can be seen in the zoomed in plot below. High-pass filters have similar physics, with the output taken across the resistor instead of the capacitor (in the physical circuit). Band-pass filters are a combination of low-pass and high-pass filters, and can be easily implemented programmatically.

• 
  Plot of the (power) gain $G(f)$ vs log frequency $\log _{10}f$ of low-pass Butterworth filters of different orders with cutoff frequency $f=1$ Hz, showing the increasing rate of frequency rejection as the order of the filters increase. Green dotted line marks cutoff frequency $f_{c}=1$ Hz.
• 
  Plot of the gain $G(f)$ vs log frequency $\log _{10}f$ of different order low-pass Butterworth filters with the cutoff point magnified, showing increasing sharpness in the cutoff behaviour as the order of the filters increase. Green dotted line marks cutoff frequency $f_{c}=1$ Hz.
• 
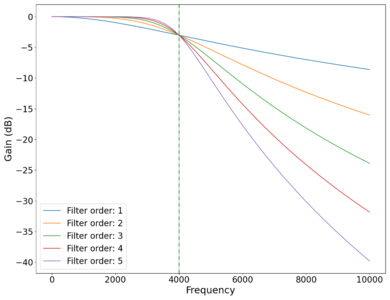
  Plot of the $G(f)$ vs frequency $f$ of different order low-pass Butterworth filters. Green dotted line marks cutoff frequency $f_{c}=4000$ Hz.
• 
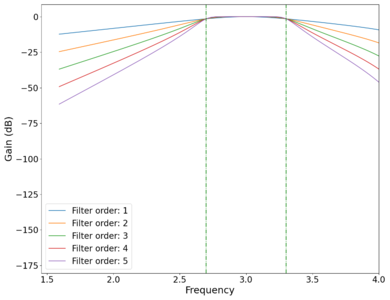
  Plot of the $G(f)$ vs log frequency $\log _{10}f$ of different order band-pass Butterworth filters. Green dotted lines mark cutoff frequencies at $100$ and $2000$ Hz.

The Butterworth filters in this work will be created using the signal package from the SciPy Python library. The butter function generates a Butterworth filter that can be specified to be low-pass, high-pass, or band-pass. An example of a band-pass filter implemented programmatically is shown above. We see slight distortions (non-zero curvature in the roll-off limit vs flat in an ideal filter) at higher frequencies due to the Nyquist frequency of the digital filter, which is a consequence of the Nyquist–Shannon sampling theorem.