Laser Microphone

A laser spot illuminating a vibrating surface should move along with it, and tracking the motion of the spot should theoretically allow us to retrieve some of the information regarding the vibrations of the surface. If a loud enough sound causes the surface to vibrate, this should theoretically be enough for the transmission of audio information through visual means. The signal obtained will then be put through a few different digital signal processing techniques in an attempt to retrieve a (good enough) copy of the original audio.

The possible applications for such a device are already covered by existing mature technologies, but the idea of transmitting raw sound information "directly" via a laser without physical connections or converting the information into a different representation based on a special protocol (e.g. Wi-Fi or Bluetooth) is in itself an interesting curiosity. In this project, we will attempt to explore the effectiveness of a simple setup made of basic electronics found around the lab in recording audio without special circuitry, and also how digital signal processing techniques can help with improving the audio obtained.

Team Members

A0166927N | Marcus Low Zuo Wu

A0171267A | Nicholas Chong Jia Le

Methods and Requirements

Using a photodiode / array of photodiodes, we attempt to record audio by measuring the signal from a laser reflecting off a surface near the sound.

Due to the nature of the setup mentioned, we require a decently dim environment to minimise noise, a visible light laser (does not need to be high powered but needs to be decently collimated), an optical bench, a set of photodiodes that can detect the laser light and produce a signal, and an electronic setup that allows us to capture and export the signal from the photodiodes.

Background

Level (logarithmic quantity)

A power level is a logarithmic quantity used to measure power, power density or sometimes energy, with commonly used unit decibel (dB).

Power level

Level of a power quantity, denoted L_P, is defined by

$L_{P}={\frac {1}{2}}\log _{\mathrm {e} }\!\left({\frac {P}{P_{0}}}\right)\!~\mathrm {Np} =\log _{10}\!\left({\frac {P}{P_{0}}}\right)\!~\mathrm {B} =10\log _{10}\!\left({\frac {P}{P_{0}}}\right)\!~\mathrm {dB} .$

where

• P is the power quantity;
• P₀ is the reference value of P.

Field (or root-power) level

The level of a root-power quantity (also known as a field quantity), denoted L_F, is defined by

$L_{F}=\log _{\mathrm {e} }\!\left({\frac {F}{F_{0}}}\right)\!~\mathrm {Np} =2\log _{10}\!\left({\frac {F}{F_{0}}}\right)\!~\mathrm {B} =20\log _{10}\!\left({\frac {F}{F_{0}}}\right)\!~\mathrm {dB} .$

where

• F is the root-power quantity, proportional to the square root of power quantity;
• F₀ is the reference value of F.

Low-pass filter

First order passive low-pass filter (top) and second order passive low-pass filter (bottom) demonstrating how higher order filters can be obtained by chaining together lower order filters.

A low-pass filter is a filter that passes frequencies lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff. Low-pass filters provide a smoother form of a signal, removing the short-term fluctuations and leaving the longer-term trend.

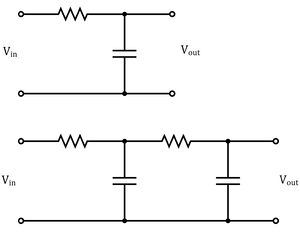
Physical RC filter

The cutoff frequency of a passive first order low-pass filter is given by

$F={1 \over 2\pi RC}$

where $R$ is the value of the resistance and $C$ is the value of the capacitance.

The top circuit on the right shows a configuration that forms such a low-pass filter. As seen on the bottom circuit on the right, higher order passive filters can be made simply by chaining together lower order filters. One issue with using a physical filter is that it adds a load to the circuit, and for higher order filters, the final output signal has a greatly decreased magnitude compared to the pure signal obtained from the photodiode. This would require the addition of amplifiers to our circuit, increasing its complexity. Additionally, from observation, the noise introduced in the connection to the oscilloscope along with electrical noise picked up by the wires is significantly greater than the noise in the signal from the photodiode itself, making an external low-pass filter performing noise filtering on the photodiode output not very effective.

As such, digital signal processing will be done instead for noise filtering. Butterworth filters specifically will be used in this work in order to minimise distortion introduced into the input.

Butterworth Filter

The Butterworth filter is a signal processing filter that is designed to have a uniform sensitivity in the passband ("desired" frequencies), while having a sufficient rejection in the stopband ("unwanted" frequencies).

The (power) gain $G(f)$ of such a filter, with a cutoff frequency $f_{c}$ and filter order $n$ is given by:

$$G(f)={\frac {1}{1+\left({\frac {if}{if_{c}}}\right)^{2n}}}$$

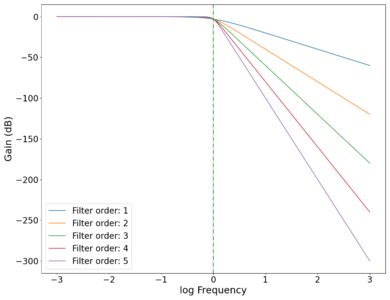
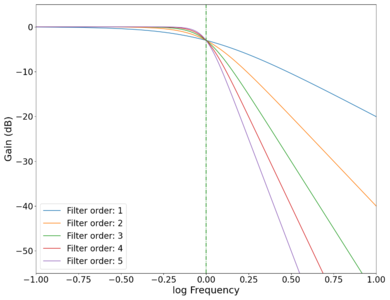
The gain curves for various orders of low-pass Butterworth filters are shown in the plot below, showing a roll-off of $-20n$ dB/decade of frequency. The roll-off at the cutoff frequency also gets sharper (roll-off starts closer to the cutoff frequency $f_{c}$ as opposed to slightly before $f_{c}$) as the order of the filter increases, as can be seen in the zoomed in plot below. High-pass filters have similar physics, with the output taken across the resistor instead of the capacitor (in the physical circuit). Band-pass filters are a combination of low-pass and high-pass filters, and can be easily implemented programmatically.

• 
  Plot of the (power) gain $G(f)$ vs log frequency $\log _{10}f$ of low-pass Butterworth filters of different orders with cutoff frequency $f=1$ Hz, showing the increasing rate of frequency rejection as the order of the filters increase. Green dotted line marks cutoff frequency $f_{c}=1$ Hz.
• 
  Plot of the gain $G(f)$ vs log frequency $\log _{10}f$ of different order low-pass Butterworth filters with the cutoff point magnified, showing increasing sharpness in the cutoff behaviour as the order of the filters increase. Green dotted line marks cutoff frequency $f_{c}=1$ Hz.
• 
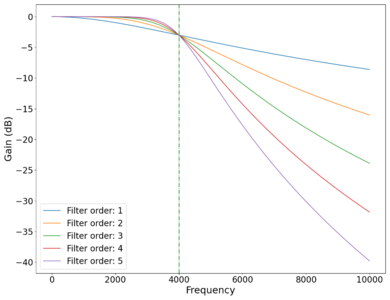
  Plot of the $G(f)$ vs frequency $f$ of different order low-pass Butterworth filters. Green dotted line marks cutoff frequency $f_{c}=4000$ Hz.
• 
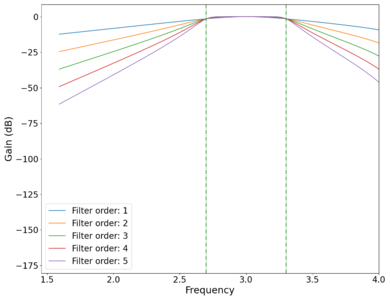
  Plot of the $G(f)$ vs log frequency $\log _{10}f$ of different order band-pass Butterworth filters. Green dotted lines mark cutoff frequencies at $100$ and $2000$ Hz.

The Butterworth filters in this work will be created using the signal package from the SciPy Python library. The butter function generates a Butterworth filter that can be specified to be low-pass, high-pass, or band-pass. An example of a band-pass filter implemented programmatically is shown above. We see slight distortions (non-zero curvature in the roll-off limit vs flat in an ideal filter) at higher frequencies due to the Nyquist frequency of the digital filter, which is a consequence of the Nyquist–Shannon sampling theorem.

An example of a band-pass 2nd order Butterworth filter implemented on white noise is seen in the image below.

Comparison between white noise (black) and filtered noise (maroon) with a 2nd order Butterworth band-pass filter applied, with the passband from 100 Hz to 1000 Hz.

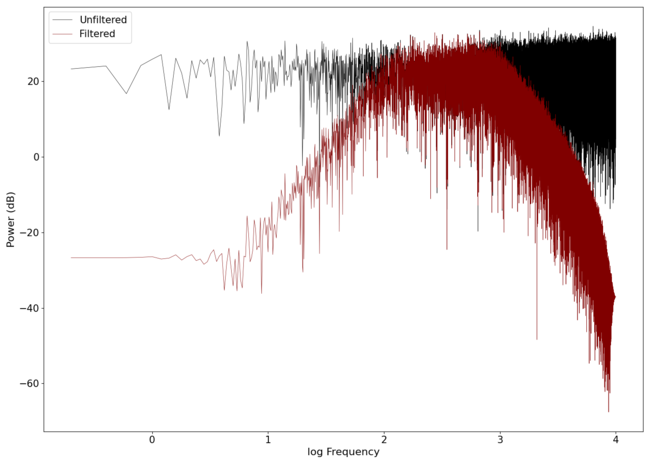
An audio comparison between the unfiltered and filtered waves can be found here: White noise and Filtered noise.

Concept

Animation demonstrating amplitude modulation. The carrier wave (top) is modulated by the the signal wave (bottom) to produce the transmitted wave (middle).

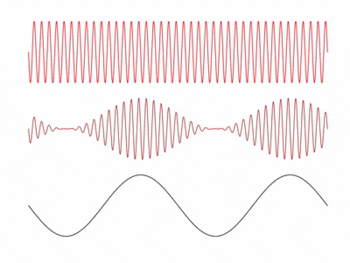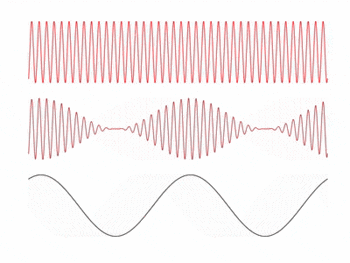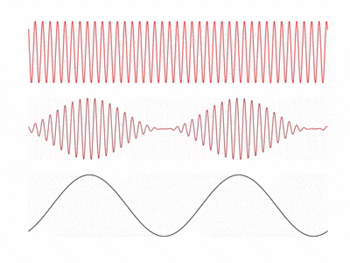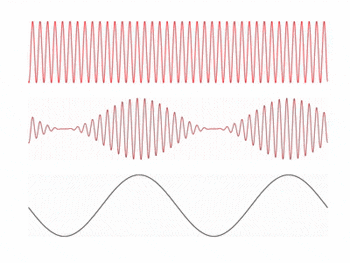
In this experiment, we attempt to convert an impinging light source into a voltage signal that reproduces an audio signal using a photodiode. The idea behind this is inspired by the concept of amplitude modulation (AM) in electronic communication. In AM, a signal (information) wave is transmitted via a carrier wave with a frequency $f_{c}$ much greater than the frequency range of the signal wave, and the receiver locks on to the frequency $f_{c}$.

The amplitude of the carrier wave is modulated by the amplitude of the signal, meaning the envelope of the transmitted wave contains the signal information. The receiver then reconstructs the signal by measuring the envelope of the received wave. An example of the three waves described is shown in the animation on the right.

In this project, a laser is reflected off a mirror attached to a surface and onto a photodiode, generating a measurable voltage. When the surface vibrates, the deflection of the mirror causes the laser to move off the photodiode, reducing the voltage to zero. Since the laser has a non-zero spot size and can be approximated to have a Gaussian profile (in the TEM₀₀ mode), intermediate levels of modulation other than 1 or 0 can also be obtained for small enough deflections.

In analogy with the amplitude modulation described above, the laser functions as a carrier wave which the photodiode is sensitive to, and the signal wave is the sound wave that causes the surface to vibrate, modulating the amplitude of the laser that reaches the photodiode. In theory, this should allow us to reconstruct the signal wave by directly converting the voltage measured into a sound wave.

The voltage measured should correspond almost directly to the envelope of the carrier wave if we use a visible light laser. This is because the frequency of visible light is in the hundreds of THz (~$10^{14}$ to $10^{15}$ Hz), while the cutoff frequency of the photodiode used is on the order of $10^{7}$ Hz. As such, the high frequency component of the carrier wave (laser) is effectively filtered out by the photodiode acting as a low-pass filter, leaving just the lower frequency amplitude modulation component in an ideal case.

Original Setup

Original setup for the laser microphone.

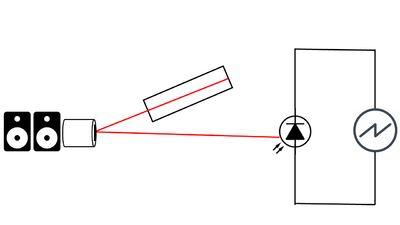
The original setup was created with as few components as possible to create a baseline performance that we can compare to. A schematic of the setup is shown in the image above. A Melles Griot HeNe laser with a wavelength of 632.8 nm was used to function as the carrier wave. The laser impinges upon a mirror attached to a surface near a pair of speakers, then gets reflected onto a photodiode which is connected to an oscilloscope. The components are shown below.

• 
  Laser connected to power supply.
• 
  Mirror mounted on original surface constructed with a balloon stretched over a 3D printed cylinder.
• 
  Laser spot on photodiode after reflection off the mirror.
• 
  Oscilloscope used to measure the signal from the photodiode.

Note that as seen in the photo of the photodiode, the laser is not centered on the photodiode but instead on one corner. We found that this improved the signal received, as this allowed small deflections to also be detected when the laser shifted in any direction, including towards the center of the photodiode (which increased the overall power on the photodiode). In contrast, if the laser is centered on the photodiode, small deflections will not be detected as the voltage output by the photodiode is only dependent on the total power received and not the location on its surface.

Modified Setup

Laser spot passing through a narrow aperture before impinging on the photodiode

We made two main modifications to our setup that led to large improvements in the quality of the recordings based on some heuristics that we observed.

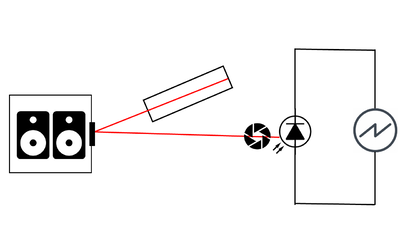
Firstly, we added an aperture in front of the photodiode to improve the sensitivity of the setup to small deviations in the laser spot location as the spot only has to move a small distance before being completely blocked by the aperture. The circular aperture also makes sensitivity of the setup isotropic relative to the direction of movement of the laser spot (as opposed to the original setup, where the response is expected to be anisotropic since the total power impinging on the photodiode depends on the direction the laser spot gets deflected in). The aperture also blocked most of the stray laser light caused by diffraction of the initial spot, which was adding substantial distortion to the recordings. The aperture is seen included within the setup in the image on the right.

Mirror mounted on a cardboard box, serving as the new vibration surface.

Secondly, we replaced the surface the mirror was mounted on with a cardboard box, as we noticed that the stretched rubber balloon had a very strong response within its resonant modes. To a first order approximation, we treat the surfaces as simply supported plates. The spacings of the modes are proportional to the square root of the elastic modulus of the material, inversely proportional to the square root of the areal density, and inversely proportional to the square of the area. As a result, we expect the new surface (which has a lower elastic modulus, larger areal density, and much larger surface area) to have closer spaced modes, which would broaden the frequency response of the surface and hopefully avoid the sharp spikes in audio at specific frequencies. The larger surface also has the added benefit of capturing a larger portion of the audio power output by the speakers, leading to more efficient conversion of the audio power to signal power.

A schematic of the new setup is seen below.

Modified setup for the laser microphone.