Orbits of the Galilean Moons

Jupiter and the four Galilean moons

Galileo Galilei’s discovery of celestial bodies that orbit something other than the Earth marked the beginning of the end of the geocentric model of the universe. In this project, we will perform the same observations on those moons as Galileo did 400 years ago.

Team Members

• A0168128Y Matthew Wee

Objectives

• To observe the planet Jupiter and its four largest moons—Io, Europa, Ganymede, and Callisto
• To measure the orbital parameters of those four moons, such as orbital period and radius
• To explore the orbital resonances of the inner three of those moons—Io, Europa, and Ganymede
• To verify Kepler’s Third Law
• To assess the viability of consumer equipment in performing precise scientific measurements

History

Animation of Galileo's observations as drawn in his book Sidereus Nuncius in 1610

Jupiter is a planet that was known to the ancients as it is the fourth brightest object in the sky behind the Sun, the Moon and Venus, and is visible to the naked eye. In 1609, astronomer Galileo Galilei made improvements to his telescope, which was the best in the world at the time. With the telescope, over the course of several weeks, he observed four “stars” moving in a line around Jupiter and was persuaded after just four days of observations that they were not stationary stars but instead objects orbiting the planet Jupiter. German astronomer Simon Marius also made this discovery independently and at the same time, but he is lesser known because he published his observations only after Galileo did. He had the privilege, however, of having his names of these moons be widely accepted, much to Galileo's dismay.

The discovery that there exist objects that do not orbit the Earth, along with several other breakthroughs, was the cornerstone of the Copernican Revolution, which was the transition from the geocentric to the heliocentric model, with the Sun instead of the Earth at the center of the universe.

Since then, astronomers have discovered a total of 80 moons that orbit Jupiter, 23 of which have no official names.

Background

The four Galilean moons, in increasing order of orbital radius, are Io, Europa, Ganymede, and Callisto, of which, Io, Callisto, and Ganymede are larger than the Earth's Moon in both mass and diameter. Ganymede is even larger than the planet Mercury. Because of their size, they can be observed from Earth with a small telescope or even a pair of powerful binoculars.

The main challenge faced when trying to observe these moons is the sheer brightness of Jupiter relative to the dim moons, and their small angular separation from Jupiter. This is especially true for the innermost moons Io and Europa.

Apparatus

Setup used to image Jupiter and its satellites

No specialized equipment was used in this experiment to make observations of the planet and its moons.

• Canon EOS 60D DSLR
  • APS-C sensor (1.6× crop)
• Sigma 150–600mm f/5–6.3
  • Lens diameter 95mm
  • Field of view: 16.4º–4.1º (effective 10.2º–2.6º)
• Low-end consumer tripod
  • Spirit level
• Remote shutter

Exposure Settings

• Manual
• Focal length: 600mm (effective 960mm)
• 1/15s exposure
• f/6.3 aperture
• ISO 3200 sensitivity
• Manual focus
• Image stabilization off

The exposure time cannot be set for too long as motion blur due to the Earth's rotation will be visible in the image.

Data

Screenshot of a camera live view of Jupiter

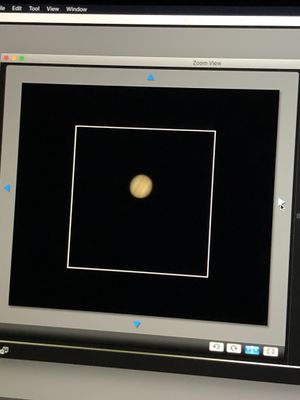
Procedure

A series of observations were performed with the telephoto lens mounted on the camera. Weather permitting, exposures were taken every day within an hour of sunset for two and a half calendar weeks from 31 January 2022 to 17 February 2022.

At the time of these observations, Earth's motion around the Sun (and to a lesser extent, Jupiter's as well) caused the apparent position of Jupiter in the sky to drift closer to the sun every day, forcing observations to occur closer and closer to sunset. The last observation on 17 February was taken at 7:59 PM, when the sun had barely set and the sky was still relatively bright (compared to the dim moons). It was decided that no more observations could be taken thereafter.

The moons in the captured images were identified using Stellarium or Night Sky.

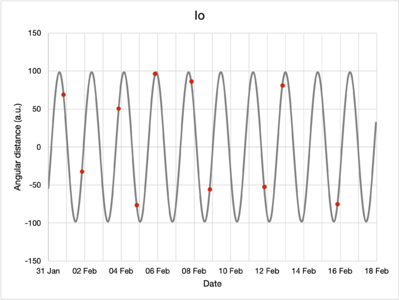
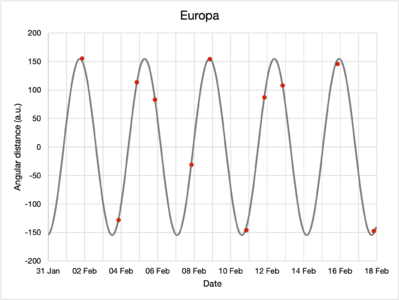
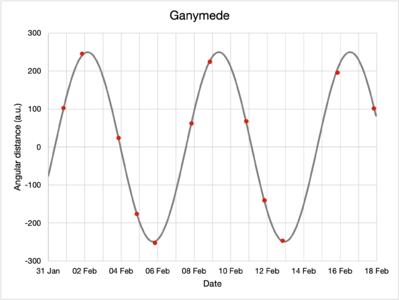
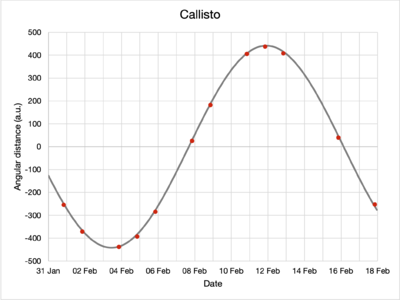
By inspecting the moons and their positions relative to Jupiter in the captured images, their apparent angular separation can be determined for every observation. The data are presented in the table below.

Raw Data

Observation	Angular distance between moon and center of Jupiter (arbitrary units)
	Io	Europa	Ganymede	Callisto
2022-01-31	68.9	occultation	102.7	-254.2
2022-02-01	-32.2	155.4	245.7	-371.0
2022-02-02	no data collected
2022-02-03	50.6	-127.9	23.8	-437.9
2022-02-04	-76.3	113.8	-175.9	-392.3
2022-02-05	96.4	83.2	-251.8	-284.4
2022-02-06	no data collected
2022-02-07	86.2	-31.0	62.2	25.5
2022-02-08	-55.7	154.5	224.8	183.0
2022-02-09	no data collected
2022-02-10	occultation	-145.8	68.0	405.6
2022-02-11	-52.4	87.2	-140.1	437.5
2022-02-12	81.0	108.1	-246.5	408.5
2022-02-13	no data collected
2022-02-14	no data collected
2022-02-15	-75.2	145.8	195.9	40.0
2022-02-16	no data collected
2022-02-17	transit	-147.2	101.8	-252.2

When a moon is occulted by Jupiter, it is not visible and its position cannot be determined with precision. Similarly, during a transit, Jupiter outshines the moon and its precise position also cannot be determined. Either way, that day's observations are not included in that moon's dataset.

Inclement weather and other circumstances have also prevented data collection on certain days as indicated.

While angular distances do not have negative values, the signs represent whether that moon has a greater or lower elevation in the sky compared to Jupiter; this helps differentiate in which part of their orbits the moons are for the purposes of modeling.

Modeling

Left: actual position of Jupiter and one of its moons as viewed from the north
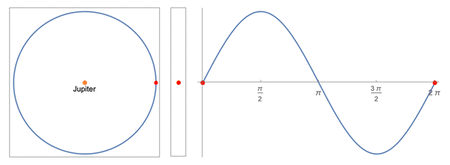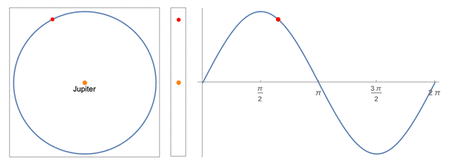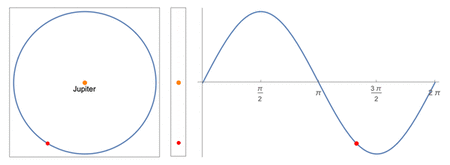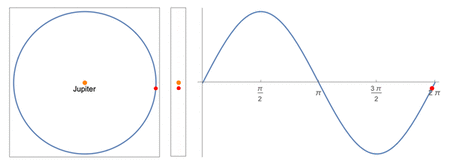
Center: apparent positions as viewed by a distant observer from Earth
Right: the apparent position plotted over time

The equation used to model the motion of the moons is

$$d\left(t\right)=a\sin \left({\frac {2\pi }{T}}\cdot t+\phi \right)$$

where $d\left(t\right)$ is the angular displacement between the moon and Jupiter as a function of time $t$, $a$ is the amplitude of the moon's oscillation about Jupiter, proportional to its semi-major axis, $T$ is the period of the orbit, and $\phi$ is the phase of the orbit.

A simple sinusoid is used to the model the moons' motions. By projecting uniform circular motion unto the plane of the sky, a pure sinusoidal wave would be obtained. In order to use this model, the following assumptions must be made:

• The inclination of the moons' orbits are 90º.
• The orbital paths of the moons are circular, and as a result
  • the moons have constant angular velocity.
  • the moons maintain a constant distance from Jupiter.
• The distance between the Earth and the Jovian system remains constant.

The validity of these assumptions will be discussed later.

Amplitude $a$ is expressed in units of pixels, but the absolute number has no physical meaning as some software was used to align the images before processing, thus one pixel no longer correlates well with a particular angular distance on the image. Time $t$ is expressed in units of calendar days from the midnight starting 31 January 2022, Singapore civil time. For example, if an observation is made on 31 January 6:00 PM, $t=0.75\mathrm {d}$. Period $T$ is also expressed in units of days (d). The phase $\phi$ serves only to fit the sinusoidal function to the data and is not physically meaningful in this analysis.

Results

The following analyses were done in Wolfram Mathematica and Microsoft Excel.

Fitted Parameters

Using the Mathematica FindFit function, the collected data were fitted to the model, obtaining the following parameters, rounded to four significant figures:

Satellite	Amplitude ${\textstyle a}$ (a.u.)	Period $T$ (d)	Phase $\phi$ (rad)
Io	98.38	1.770	5.701
Europa	154.7	3.555	4.807
Ganymede	249.3	7.196	5.975
Callisto	441.7	16.92	3.433

Angular distance is expressed in arbitrary units (a.u.), not astronomical units (AU).

Plots

• Plots of Observations and Fitted Models
• 
• 
• 
• 

The red dots plot the observations made while the grey lines denote the fitted model. Note the differences in vertical axis scaling.

Comparisons with Literature Values

Visually, from the plots, the model of the moons' motions seem to fit the observed data well.

Orbital Period

Satellite	Observed Period (d)	Actual Period (d)	Discrepancy
Io	1.770	1.769	0.063%
Europa	3.555	3.551	0.104%
Ganymede	7.196	7.155	0.570%
Callisto	16.92	16.69	1.407%

The discrepancies between the empirical data and the literature values are small but increase with increasing period.

Orbital Radii

Because the distance to Jupiter is not known in this exercise, the actual orbital radius (in actual distance units) of each moon cannot be inferred from the observations alone. Instead the ratios of the orbital radii of the three outer moons to Io are taken and compared to the literature values.

Satellite	Observed Amplitude (a.u.)	Observed Ratio (relative to Io)	Actual Semi-major Axis (km)	Actual Ratio (relative to Io)	Discrepancy
Io	98.38	1	422 000	1	-
Europa	154.7	1.573	671 000	1.590	1.079%
Ganymede	249.3	2.534	1 070 000	2.536	0.075%
Callisto	441.7	4.490	1 883 000	4.462	0.625%

Again, the discrepancies between the empirical data and the literature values are small.

Orbital Resonance

By expressing the orbital periods in multiples of the period of Io, the orbital resonance phenomenon between Io, Europa, and Ganymede can be identified.

Satellite	Observed Period (relative to Io)	Actual Period (relative to Io)	Discrepancy
Io	1	1	-
Europa	2.008	2.007	0.041%
Ganymede	4.065	4.045	0.506%
Callisto	9.561	9.434	1.343%

The relative periods between the three innermost moons are small integer multiples of each other—characteristic of bodies in orbital resonance. The oscillating gravitational influence they experience between themselves is a stable interaction that ensures their relative positions maintain over time. Callisto does not seem to participate in this arrangement.

Kepler's Third Law

Log-log plot of observed period against orbital radius; the grey line connecting the four points representing the moons illustrates Kepler's third law

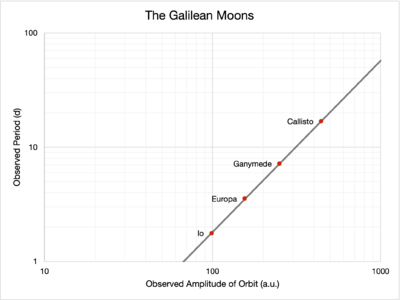
Kepler's third law of planetary motion, in mathematical terms, reads that for all objects orbiting the same primary massive object,

$$T^{2}\propto a^{3}$$

where $T$ is the period of the orbit and $a$ is the semi-major axis of the orbit.

Kepler published these laws with the Sun and planets in mind (hence "Kepler's laws of planetary motion"), but they also apply to moons orbiting planets as well.

Satellite	Observed Amplitude (a.u.)	Observed Period (d)	Constant of proportionality ${\frac {a^{3}}{T^{2}}}$
Io	98.38	1.770	303 900
Europa	154.7	3.555	293 300
Ganymede	249.3	7.193	299 100
Callisto	441.7	16.92	301 000

Derivation

By equating Newton's Law of universal gravitation with centripetal acceleration,

$$mr\omega ^{2}=G{\frac {Mm}{r^{2}}}$$

where $m$ is the mass of the moon, $r$ is the radius of the moon's orbit, $\omega$ is the angular velocity of the moon, $G$ is the gravitational constant, and $M$ is the mass of Jupiter.