Contactless Conductivity Measurement

Introduction

In our Spintronics Lab, when we want to analyze a sample, conductivity or resistivity as a electrical property is almost always necessary. Normally, we use a Voltmeter or standard four probes method to take a measurement. However, surface preparation and contamination have great effects on the electrical properties of the samples. Thus, a contactless technic would be a better way to carry out the conductivity measurement. When we were doing the ac magnetic susceptibility measurement, we learn from literature that there is connection between the electrical conductivity and the ac magnetic susceptibility. We would like to build the set up from the literature, take a measurement on the conductivity of our metal sample and compare it with the result from standard four probes measurement.

Theory

The mechanism for the contactless conductivity measurement is identical to the effective magnetic susceptibility measurement. Basically, the sample is inserted into a primary coil and a secondary coil. An ac current passes through the primary windings will induce magnetic field. The sample responds to the magnetic field and eddy current will be induced within the sample. Then, EMF will be induced in the secondary coil due to not only the driving magnetic field of the primary coil, but also the magnetic field of the currents induced in the sample. Two magnetic fields are 90 degrees out of phase so that the real part and imaginary part of the resultant voltage will be separately related to the ac magnetic susceptibility and the conductivity. When calculating the conductivity from voltage, there are two different approaches introduced by Ishida et al. and Iñiguez et al..

The first approach uses susceptibility to express the magnetic flux penetrating the cylindrical sample and relate the magnetic flux to EMF. It gives rise to the final expressions

${\begin{alignedat}{2}v_{p}&=4\pi G\chi _{0}a^{2}lfH_{0}\\v_{q}&={\frac {1}{4}}\pi \mu _{0}G\sigma a^{4}lf^{2}H_{0}\end{alignedat}}$

which $v_{p}$ is the real part of the induced voltage and $v_{q}$ is the imaginary part. $\chi _{0}$, $\mu _{0}$, $\sigma$, $a$,$G$, $l$ are the susceptibility, permeability, conductivity, radius, geometric coefficient and length of the cylindrical sample. $f$, $H_{0}$ are the frequency and strength of the primary coil magnetic field. Some parameters can be reduced or cancelled out when we divide the two voltages and the equation we eventually use is

${\begin{alignedat}{2}\sigma &={\dfrac {v_{q}}{v_{p}}}{\dfrac {16\chi _{0}}{\mu _{0}a^{2}f}}\end{alignedat}}$

The second approach uses root mean square voltage measured with without sample to calculate conductivity. It gives rise to the expression

${\begin{alignedat}{2}\tan(\phi )&={\dfrac {\mu _{0}\pi }{8}}(D^{2}-d^{2})\sigma f\end{alignedat}}$

which $\phi$ represent the phase shift come after inserting sample into coils. We assume V_1,rms is the voltage without sample and V_2,rms is the one with sample.

${\begin{alignedat}{2}\cos(\phi )&={\dfrac {V_{1},rms}{V_{2},rms}}\end{alignedat}}$

And D and d are the outer and inner diameter of the sample because this approach chooses tube sample. When we express it in terms of voltages, the expression becomes

${\begin{alignedat}{2}\sigma &=\tan(\phi ){\dfrac {8}{\mu _{0}\pi (D^{2}-d^{2})f}}\end{alignedat}}$

We used both methods for the material in the experiment to compare their results with same experiment set up.

To do list

Prepare the samples

Prepare the coils

Build the experimental set up

Measure

Graph and Report

Sample Preparation

For this experiment, we have tested three samples, copper metal rod (Cu), Teflon sodium doped lanthanum manganite (La_1-xNa_xMnO₃). We choose copper and Teflon because we have them in the workshop and the theoretical values of some necessary parameters like susceptibility and conductivity of copper and Teflon are easy to obtain online so that we can calculate and verify our results. We also choose La_1-xNa_xMnO₃ especially La_0.95Na_0.05MnO₃ because we have measured its resistivity value through standard four probes method in our MPT projects. Due to its property of changing Curie temperature with respect to the level of doping, La_0.95Na_0.05MnO₃ at room temperature shows metallic like resistivity behavior.

The copper rod we cut and polished is presented in Figure 1. The radius of the rod is 0.005 meters and the length is 0.0082 meters. The theoretical volume susceptibility we found online is -9.63 * 10^-6 and the conductivity is about 58.7 * 10⁶ siemens/meter. We will use these parameters as well as our measured voltage to compute our experimental conductivity. Teflon is cut with the same dimension with theoretical conductivity about 10^-24 siemens/meter.

Figure 1. A picture of our copper rod sample

To synthesize La_0.95Na_0.05MnO₃, we use solid-state Microwave Synthesis due to its advantages in short reaction time, low energy consumption and clean reactions. We first take the La₂O₃, Na₂CO₃ and Mn₂O₃ in correct molecular ratio, grind and mix them together, then put the powder into microwave furnace for heating. The temperature is raised to the desired temperature in 20 min with a fixed MW power and the powder is maintained at the final temperature for 30 min for reactions to complete and then the power is switched off. The samples cool to room temperature in 1 hour. After that, the powder was grinded again and the process was repeated for the 2nd time for homogenization. Finally, we press the powder into pellet and subjected to MW irradiation for the 3rd time. The heating temperature and power we use are 1000 degrees Celsius and 1000 Watts. The resistivity of this sample measured by four probes method is about 0.5 Ohm * centimeter.

Figure 2. A picture of our La_0.95Na_0.05MnO₃ sample

Figure 3. A picture of us grinding the sample

Experiment Set up

The measuring circuit consists of a detecting coil, a compensating coil with equal turns of copper wire and a primary coil. The primary coil is connected to the Lock-in Amplifier output. Ac current flows through primary coil and gives rise to magnetic field. The detecting coil and the compensating coil are connected to Lock-in Amplifier input so that we can measure the voltage. The compensating coil is used to compensate the voltage in detecting coil without samples. We connect the detecting coil to one port in Lock-in Amplifier and compensating coil in another port. The resultant voltage is the difference between two coils which is the voltage induced by the Eddy current in the sample. Of course, the sample is placed within detecting coil and the sample length is short compare to the length between detecting coil and compensating coil so that the Eddy current in the sample has little effect on the compensating coil. In literature, secondary coil is adjusted in position and voltage offset so that voltage without sample is zero. The combination of detecting coil and compensating coil in our set up is analogous to the secondary coil used in literature. Figure 4 shows our coils and different terminals. Two terminals on the right are the positive and negative terminals for primary coil. The magnetic field induced by this coil is calculated to be 14.073 * I which I is the applied current controlled by the Lock-in Amplifier. There are three terminals on the left. We connect upper two to for the detecting coil and lower two for the compensating coil. They are connected to different input ports in Lock-in Amplifier. We put tissues in the bottle so that the sample lies in the range of detecting coil

Figure 4. A picture of our winded coil

Figure 5 shows the coils connected to wires and Figure 6 shows how they are connected to SR830 Lock-in Amplifier

Figure 5. A picture of coils connecting the wires

Figure 6. A picture of wires connecting SR830 Lock-in Amplifier

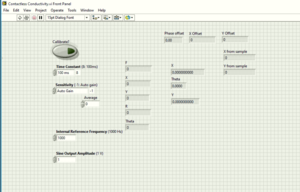
Figure 7 shows the panel of the Labview program we built. First, We do one measurement without samples, the program will give us some x, y and theta values. Ideally, the theta value would be 0 because we have the compensating coil. But in reality, the coils are not perfect so that we need to calibrate the system to cancel the phase. The calibration is done by giving some offsets so that theta becomes 0. This is automatically done when we choose the "calibrate" option in the program for the first measurement. Then we insert our samples and measurement with calibrate option off. The "x from sample" and "y from sample" in the program will give us the final results which correspond to real and imaginary part of the EMF induced by the sample.

Figure 7. A screenshot of the Labview program panel we built to calibrate and measure

Data Analysis

We first measure the copper rod with diameter of 6mm under low frequency range and high frequency range separately both under AC current with amplitude of 1V. The imaginary response in voltage didn't show the quadratic dependence of frequency frequency. Instead both Vp and Vq shows a linear variation with frequency like in Fig.1 which we suppose to be the intrinsic frequency dependence of ac conductivity. As a result the conductivity of Cu rod shown in Fig3 decreases with the increase of frequency which shows a similar value with dc conductivity. around kHz range.

In addition, we measured Teflon, an insulator, for comparison. According to the conductivity vs. f in Fig4, we can observe alternating positive and negative values with even a singular point. Both Vx and Vy collected from lock-in amplifier shows alternating positive and negative values as well with absolute value in the same magnitude with calibration data.As a result , we believe Teflon induces so weak response to the alternating current that we can hardly measure its ac conductivity.

Another sample we measured is La_0.95Na_0.05MnO₃ which is the ferromagnetic insulator at temperature. The conductivity we measured at tens of kHz range is several orders of magnitude higher than the dc conductivity we measured with the standard four probe method. As it's the insulator, the response is weak as well compared to copper rod, which will lead to the inaccuracy of the ac conductivity. Besides, skin depth is much smaller for this sample due to the ferromagnetic nature which will lead to the nonuniform distribution of eddy current in the samples. This will be in contrast with our assumption that eddy current should be uniformly distributed in the sample when we calculate the conductivity. This may be the reason why we get much higher value than dc conductivity.

We finally measured the copper rod with the second method mentioned in theory part to compare with results from copper rod. We measured the V_rms before and after inserting the sample in to the coils. And we calculated the phase shift from V₁ and V₂ which finally give the conductivity. Similar result comes in this experiment that ac conductivity shows similar value with dc conductivity around kHz range and shows the frequency dependence.

Team Members

Chen Guohao, Jiang Luwen

Lab Location

Spintronics and Magnetic Materials Lab

References

Bean, C. P., DeBlois, R. W., & Nesbitt, L. B. (1959). Eddy‐Current method for measuring the resistivity of metals. Journal of Applied Physics, 30(12), 1976-1980. https://doi.org/10.1063/1.1735100​

Crowley, J. D., & Rabson, T. A. (1976). Contactless method of measuring resistivity. Review of Scientific Instruments, 47(6), 712-715. https://doi.org/10.1063/1.1134714​

Oike, H., Miyagawa, K., Kanoda, K., Taniguchi, H., & Murata, K. (2009). Contactless conductivity measurements on the organic conductor, κ-(ET)4Hg2.89Br8, under pressure. Physica. B, Condensed Matter, 404(3-4), 376-378. https://doi.org/10.1016/j.physb.2008.11.023

Kraftmakher, Y. A. (1991). Measurement of electrical resistivity via the effective magnetic susceptibility. Measurement Science & Technology, 2(3), 253-256. https://doi.org/10.1088/0957-0233/2/3/011

Bauhofer, W. (1977). Continuous, contactless measurement of the temperature-dependent electrical resistivity of metals. Journal of Physics. E, Scientific Instruments, 10(12), 1212-1214. https://doi.org/10.1088/0022-3735/10/12/003