Custom atomic beam source
Team Members and Lab location
Lu Tiangao, Li Putian in S14-03 Travis's Lab
Introduction
In this report, we introduced an atomic oven designed by ourselves. The whole design will be suitable for atoms that need temperature ranging from 500K to 1300K. The idea came from our lab's commercial atomic beam source was both expensive and having some defects.
Theory part
Vapor Pressure
Indium is the group III atom, and it has two stable isotopes In-113 and In-115, the atom we use is In-115 with an abundance of 95.7%, the melting point is 156.6°C. To calculate the density of atoms coming from the nozzles. We should know the pressure and temperature of the gas, which the density formula is given by:
When a material is in thermodynamic equilibrium with its vapor at a given temperature in a closed system, the pressure at this time is called vapor pressure. The vapor pressure of indium is given by
We can plot the vapor pressure with Temperature range from 800°C to 1000°C:
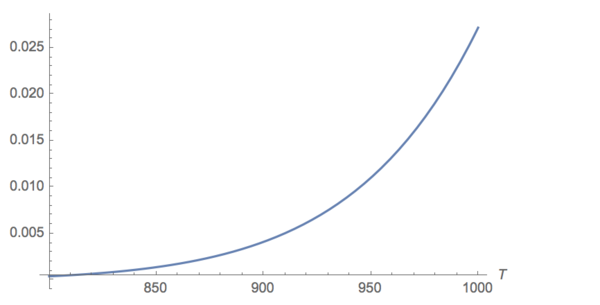
A pressure of 1e-3 torr is a number typically used in many cold atom experiments. Thus we get the temperature around 833.82°C is the suitable temperature of indium atom experiment. Then, according to the density formula, we can get the density of atoms inside the crucible is
Maxwell distribution
Firstly, indium atoms inside the crucible will obey the Maxwell-Boltzmann distribution.
Failed to parse (unknown function "\begin{alignat}"): {\displaystyle \begin{alignat}{2} f_{MB}(v)dv=\sqrt{\frac{2}{\pi}}\frac{v^2dv}{\sqrt{k_B T/m}^3}e^{-mv^2/{2k_B T}}, \quad \int_0^{v_{ini}} f_{MB}(v)dv \sim 53.3\ \end{alignat} }
However, when considering the speed distribution of the atoms coming out of the nozzle, we should add another factor of v into the distribution function. Because the gas atoms emerging outside of the small apertures cannot be representative of the atoms inside the crucible.\cite{thermalphysics} So the distribution function of the outside atoms is given by:
Failed to parse (unknown function "\begin{alignat}"): {\displaystyle \begin{alignat}{2} f(v)dv={\frac{1}{2}}\frac{v^3dv}{{(k_BT/m)}^{2}}e^{-mv^2/{2k_B T}}, \quad \int_0^{v_{ini}} f(v)dv \sim 36.3\ \end{alignat} }
Custom oven design
Items needed
- Custom Flange feedthrough
- Thermocouples and thermocouple feedthrough
- Tantalum heating wires and current feedthrough
- Crucible and nozzle
- PBN holding rings
- Vacuum Flange, cube and viewports
- Heating wire power system
- Cooling system for oven
Oven setup
- Wiring practice
- Washing parts for vacuum


